LiNGAMによる因果探索(応用編)#
LiNGAMによる因果探索(基本編)では因果探索におけるモデルの一つであるLiNGAM、およびそのパラメータ推定手法[2]DirectLiNGAMについて紹介し、lingamライブラリを用いた因果グラフの推定・可視化まで行いました。本稿ではその応用編として、DirectLiNGAMの推定結果の解釈や、DirectLiNGAMを実際のデータに適用する際に必要となる前処理、推定結果の信頼度評価の方法について説明します。また、付録にて事前知識を利用する方法についても紹介します。
必要なライブラリのインポート・推定の実行まで#
注意
本稿の実行例ではlingamライブラリv1.8.2を利用しており、解説もこのバージョンでの実装に基づいて行います。
まずはLiNGAMによる因果探索(基本編)の実験パートと同様の手順で下図のモデルに従う人工データを生成したのち、それに対してDirectLiNGAMで推定を行うところまで実行していきます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx
from scipy import stats
import lingam
import warnings
warnings.filterwarnings('ignore') # Warningを無視する
# lingamのバージョン確認
print(lingam.__version__)
1.8.2
# ノイズX, 因果グラフGからデータセットを生成する関数
def noise_to_causal_data(X, G):
out = X.copy()
for v in nx.topological_sort(G):
for u, d in G.pred[v].items():
out[v] += d['weight'] * out[u]
return out
# 真の因果グラフGtrueの定義
Gtrue = nx.DiGraph()
Gtrue.add_nodes_from([fr'$x_{i}$' for i in range(1,5)])
Gtrue.add_weighted_edges_from([
('$x_1$', '$x_3$', -1),
('$x_2$', '$x_1$', 1),
('$x_2$', '$x_3$', 2),
('$x_2$', '$x_4$', 1)
])
e_label_dict_true = {(i, j): f'{d["weight"]:.1f}' for i, j, d in Gtrue.edges(data=True)}
e_width_list_true = [ abs(d['weight']) for (u, v, d) in Gtrue.edges(data=True)]
# 人工データセットの作成
n = 1000
np.random.seed(1)
# Xの各列に独立なノイズを入れる
X = pd.DataFrame(data=np.random.uniform(low=-1.0, high=1.0, size=(n, 4)), columns=Gtrue.nodes())
X = noise_to_causal_data(X, Gtrue)
# 因果グラフの推定
l = lingam.DirectLiNGAM().fit(X)
ここまでで、人工データの生成およびDirectLiNGAMによる因果グラフの推定までが完了しました。LiNGAMによる因果探索(基本編)ではここから因果グラフの可視化を行いましたが、今回は因果順序や隣接行列、総合効果の可視化および結果の信頼度評価を行います。
なお本稿の実行例では以後、上で生成したXを用いて分析を行います。
隣接行列#
fitメソッドで因果グラフを推定した後、adjacency_matrix_で隣接行列にアクセスできます。
# 隣接行列
print(l.adjacency_matrix_)
[[ 0. 1.05671176 0. 0. ]
[ 0. 0. 0. 0. ]
[-0.95838879 1.9550515 0. 0. ]
[ 0. 1.01647299 0. 0. ]]
隣接行列はLiNGAMを
と行列表示した際の\(\mathbf{A}\)となります。すなわち、隣接行列の第\((i, j)\)成分は因果グラフにおける辺\(x_j \to x_i\)の重みとなります。
注意
この隣接行列は一般にグラフ理論で隣接行列と呼ばれるものとは少し異なります。グラフ理論における隣接行列\(\mathbf{A}_\text{graph}\)は第\((i,j)\)成分が辺\(x_i \to x_j\)の有無、あるいは重みを表すものですが、LiNGAMにおける隣接行列\(\mathbf{A}_\text{LiNGAM}\)の第\((i, j)\)成分は因果グラフにおける辺\(x_j \to x_i\)の重みを表しています。そのため、グラフ理論における隣接行列\(\mathbf{A}_\text{graph}\)とLiNGAMにおける隣接行列\(\mathbf{A}_\text{LiNGAM}\)の間には
の関係があります。グラフを取り扱うライブラリ、例えばNetWorkXでは隣接行列からグラフを作成する際にグラフ理論における隣接行列\(\mathbf{A}_\text{graph}\)を要求するので、\(\mathbf{A}_\text{LiNGAM}\)を使ってNetworkXなどでグラフを作成する際には転置をとった\(\mathbf{A}_\text{LiNGAM}^T\)を渡してやる必要があります。(本稿やLiNGAMによる因果探索(基本編)の実行例では、実際に\(\mathbf{A}_\text{LiNGAM}^T\)を渡してグラフを生成しています。)
直接効果と総合効果#
先ほど、DirectLiNGAMで推定される隣接行列の第\((i,j)\)成分\(a_{ij}\)は因果グラフにおける辺\(x_j \to x_i\)の重みである、と説明しました。すなわち\(x_j\)を\(1\)増やすと\(x_i\)が\(a_{ij}\)増加するという意味合いがありますが、この表現にはやや語弊があります。なぜなら実際に\(x_j\)を\(1\)だけ増やした際には辺\(x_j \to x_i\)により\(x_i\)を直接変化させる直接効果に加えて、\(x_j\)から他の変数\(x_k, x_l, \dots\)を経由する\(x_j \to x_k \to x_l \to \cdots \to x_i\)のパスを通って\(x_i\)を変化させる間接効果が存在する可能性があり、もし間接効果が存在すれば\(x_j\)を\(1\)増やした際の\(x_i\)の増加量は\(a_{ij}\)に間接効果を加えた量となるためです。
例えば、先ほど用意した人工データの因果グラフを再掲して見てみましょう。
ここで例えば\(x_2\)を\(1\)増やした際の\(x_3\)への影響は
辺\(x_2 \xrightarrow{2} x_3\)により\(x_3\)を\(2\)増加させる直接効果
パス\(x_2 \xrightarrow{1} x_1 \xrightarrow{-1} x_3\)により\(x_3\)を\(1 \times (-1) = -1\)増加(=\(1\)減少)させる間接効果
が合わさり「\(x_3\)は\(1\)増加する」という結果となります。
このように直接効果・間接効果を合わせた「\(x_j\)を\(1\)増やした際の\(x_i\)の増加量」を\(x_j\)から\(x_i\)への総合効果と呼びます。この言葉を使うと上の例は「\(x_2\)から\(x_3\)への総合効果は\(1\)である」と言い換えることができます。
lingamライブラリでは因果グラフ推定後にestimate_total_effectメソッドで2変数間の総合効果を計算できます。
# インデックス1から2(x_2からx_3に対応)への総合効果の算出
l.estimate_total_effect(X, from_index=1, to_index=2)
0.9423107945490131
今回のデータではインデックス1から2、すなわち\(x_2 \to x_3\)の真の総合効果は先述の通り\(1\)であるため、概ね正しく推定できていることが確認できます。
前処理(標準化)#
DirectLiNGAMを用いる際には、因果グラフの推定精度を上げるための前処理として標準化を行うことが重要です。
標準化が重要である原因の一つとしては、LiNGAMの係数が変数のスケールに依存することが挙げられます。LiNGAMの特徴として、変数のスケールを大きくするとその変数からの直接効果は小さく見積られ、逆にスケールを小さくするとその変数からの直接効果は大きく見積られる、というものがあります。そうなると、例えばある目的変数に対してどの変数が主な原因であるかを係数の絶対値の大小で判断する際、変数のスケールによって結果が変わってしまいます。変数のスケールは例えば下図のように違う単位を使うだけで変化してしまいますので、どの単位を使っても結果が変わらないように標準化を行う、というのが理由の一つです。
また、標準化を行うもう一つの理由としてDirectLiNGAMの推定アルゴリズム内で必要になるから、ということも挙げられます。DirectLiNGAMの推定アルゴリズムはLiNGAMによる因果探索(基本編)で解説したように大きく分けて(1)因果順序の推定、(2)係数の推定からなります。(2)の係数の推定手法は特に限定されていませんが、例えばlingamライブラリではadaptive Lassoが用いられています。この場合、adaptive Lassoでは前処理で標準化を行うことが一般的ですので、やはり前処理で標準化は行う方がよいでしょう。
注釈
lingamライブラリv1.8.2を使用する際は、パラメータ推定を行うDirectLiNGAM.fitメソッドの中に標準化を行う処理が含まれているので、前処理で標準化を行う必要はありません。ただし、その場合でも前処理での標準化の有無によって推定された隣接行列の意味合いが変わるため、分析の目的に応じて標準化の有無を使い分ける必要があります。
まず前処理で標準化を行わない場合、推定された隣接行列の第\((i, j)\)成分\(a_{ij}\)は因果グラフにおける辺\(x_j \to x_i\)の重み、すなわち「\(x_j \to x_i\)の直接効果」を表します。ですので例えば\(x_j \to x_i\)の直接効果や総合効果を知りたいときは、標準化を行わずに推定することになります。
一方で前処理で標準化を行う場合、推定された隣接行列の第\((i, j)\)成分\(a_{ij}\)は元の\(x_j \to x_i\)ではなく標準化後の変数\(z_i = (x_i-\mu_i) / \sigma_i,\ z_j = (x_j-\mu_j) / \sigma_j\)間の直接効果を表すことになります。標準化ありで推定を行うケースとしては例えば、\(x_i\)の原因となる変数の重要度を知りたいときが挙げられます。変数の重要度を比較する際は隣接行列の成分(の絶対値)の大小を比較するので、スケールの違いで結果が変化しないように標準化を行います。
DirectLiNGAMの結果の信頼度評価#
DirectLiNGAMを実データに対して用いた際、推定された因果グラフがどの程度正確に真の因果関係を表現できているかは気になるところです。しかしDirectLiNGAMのような因果探索手法では一般的に推定精度の評価が困難です。例えば回帰問題では予測すべき目的変数の値がデータで与えられているので、それとモデルの予測値から予測誤差を平均二乗誤差や平均絶対誤差などの指標で評価できました。しかし、DirectLiNGAMで因果グラフを推定する際は人工データなどでない限り真の因果グラフは基本的に未知ですので、回帰問題のように推定した因果グラフを真の因果グラフを比較して誤差を評価することはできません。
そこでここでは、DirectLiNGAMにおいて結果の信頼度を評価するための手法として
ブートストラップ法
ノイズの独立性検定
ノイズの正規性検定
を紹介します。
ブートストラップ法#
ブートストラップ法とは、データからの重複を許したランダム抽出(復元抽出)により得た各再標本(ブートストラップサンプル)に対して推定量を計算することで、推定量の分散や信頼区間などを求める手法です。
DirectLiNGAMにおいては、ブートストラップ法を用いることで辺\(x_j \to x_i\)の出現確率を計算し、辺の信頼度評価を行ったりすることができます。例えば100回ブートストラップを行った際、辺\(x_j \to x_i\)が100回中2~3回しか出現しないようなら\(x_j \to x_i\)の因果関係は実際には存在しない可能性が高く、逆に辺\(x_j \to x_i\)が100回中ほぼ毎回出現するようなら\(x_j \to x_i\)が真の因果関係である可能性は高い、といった具合です。
ここでは、lingamライブラリに実装されているブートストラップ法を実際に試してみます。lingamライブラリの実装ではまず、サンプル数\(n\)のデータを与えると同じくサンプル数\(n\)の再標本をn_saplingで指定した回数だけ復元抽出します。その後、得られたn_sapling個の再標本それぞれについてDirectLiNGAMで推定を行った結果を格納したlingam.bootstrap.BootstrapResult型のオブジェクトを返します。
# ブートストラップの実行
bs_result = l.bootstrap(X, n_sampling=100)
print(type(bs_result))
<class 'lingam.bootstrap.BootstrapResult'>
上のコードで、bs_resultにブートストラップの結果が格納されました。今回はn_sampling=100なので100個の再標本に対する推定結果が得られたことになります。まずはブートストラップ法の理解を深めるために、いくつかの再標本について推定結果のDAGを確認してみます。
# 最初の10個の再標本についての推定結果(DAG)を可視化
# 各変数の表示位置の指定
pos = {
'$x_1$': (-1, 1),
'$x_2$': (1, 1),
'$x_3$': (-1, -1),
'$x_4$': (1, -1)
}
fig, axes = plt.subplots(2, 5, figsize=(25, 10))
for i, ax in enumerate(axes.ravel()):
G = nx.from_numpy_array(bs_result.adjacency_matrices_[i].T, create_using=nx.DiGraph()) # i番目の再標本に対する推定結果(隣接行列)からグラフを生成
G = nx.relabel_nodes(G, {v: fr'$x_{i+1}$' for i, v in enumerate(G.nodes())})
e_label_dict_est = {(i, j): f'{d["weight"]:.4f}' for i, j, d in G.edges(data=True)}
e_width_list_est = [ abs(d['weight']) for (u, v, d) in G.edges(data=True)]
ax.set_title(f'Resample {i}')
nx.draw_networkx_nodes(G, pos, ax=ax, node_size=600, node_color='#ffaaaa', edgecolors='k')
nx.draw_networkx_edges(G, pos, ax=ax, width=e_width_list_est, style='solid', arrowstyle='->', node_size=600, arrowsize=20)
nx.draw_networkx_labels(G, pos, ax=ax)
nx.draw_networkx_edge_labels(G, pos, edge_labels=e_label_dict_est, ax=ax, rotate=False)
fig.show()
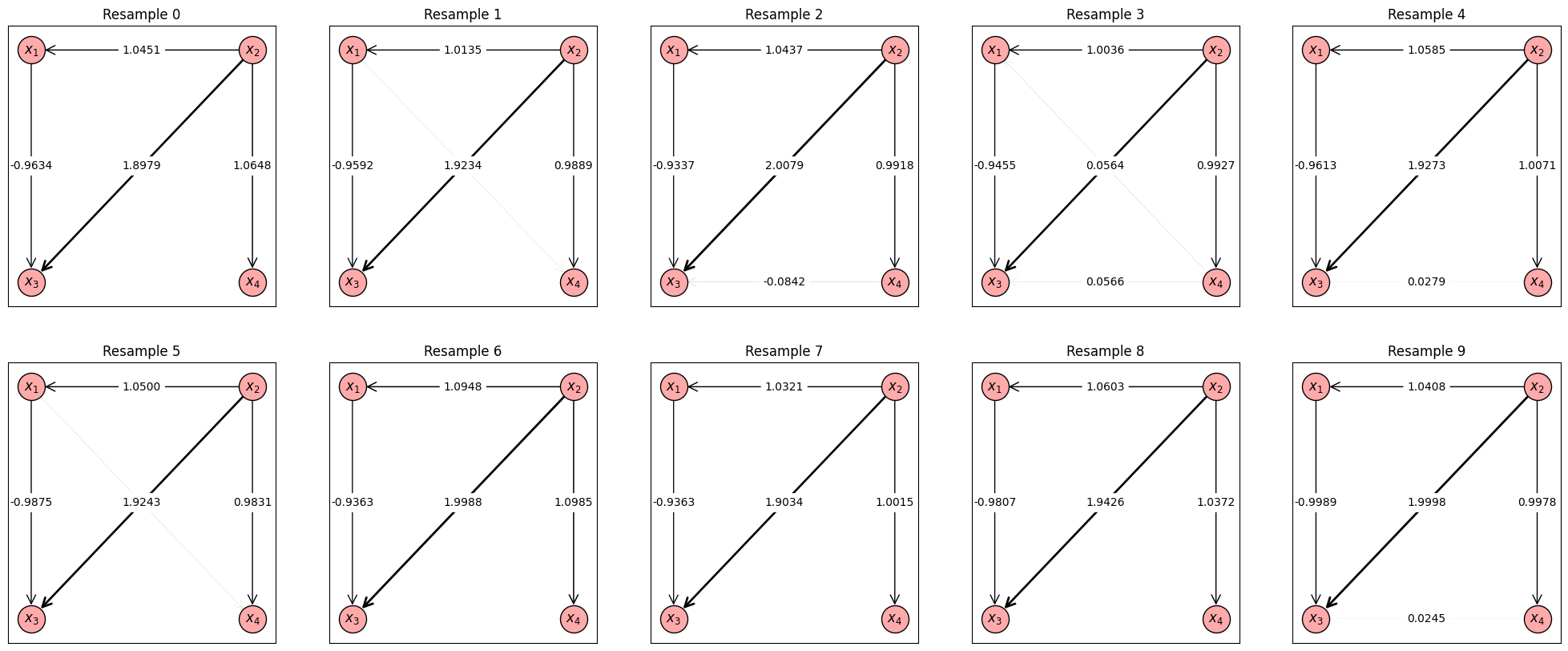
上の出力結果は最初の10個の再標本に対する推定結果のDAGを並べたものです。実際には再標本を100個生成しているので、あと90個の再標本についての推定結果も計算されています。以下では、これらの推定結果から辺や総合効果の出現率を計算して信頼度評価を行います。
まずは辺の出現数を計算してみます。
# 辺の出現数。辺from -> toがcount回だけ出現したことを示している。結果はcountが多いものから順に並んでいる。
pd.DataFrame(bs_result.get_causal_direction_counts())
| from | to | count | |
|---|---|---|---|
| 0 | 1 | 0 | 100 |
| 1 | 0 | 2 | 100 |
| 2 | 1 | 2 | 100 |
| 3 | 1 | 3 | 100 |
| 4 | 0 | 3 | 31 |
| 5 | 3 | 2 | 27 |
| 6 | 3 | 0 | 11 |
| 7 | 2 | 3 | 5 |
上の計算結果は各辺の出現数を表しています。例えば結果の一番下の行は、インデックス2から3(\(x_3 \to x_4\)に対応)の辺が100回中5回出現したことを意味しています。このことから、\(x_3 \to x_4\)の因果関係は実際には存在しない可能性が高いと評価できます。実際、今回の人工データでは\(x_3 \to x_4\)に直接的な因果関係は存在しません。逆に、結果の上から1~4行目を見ると辺\(x_2 \to x_1, x_1 \to x_3, x_2 \to x_3, x_2 \to x_4\)は100回中100回出現していることが分かるため、これらの4辺は真の因果関係である可能性が高いと評価でき、実際このデータではこれらの4辺は真の因果関係です。
続いて、総合効果の集計結果を見ていきます。
# 総合効果。from -> toの総合効果が確率probabilityで現れ、現れた総合効果の中央値がeffectであったことを示している。
pd.DataFrame(bs_result.get_total_causal_effects())
| from | to | effect | probability | |
|---|---|---|---|---|
| 0 | 1 | 0 | 1.059640 | 1.00 |
| 1 | 0 | 2 | -0.960564 | 1.00 |
| 2 | 1 | 2 | 0.938568 | 1.00 |
| 3 | 1 | 3 | 1.017397 | 1.00 |
| 4 | 0 | 3 | 0.047163 | 0.32 |
| 5 | 3 | 0 | 0.061070 | 0.11 |
| 6 | 3 | 2 | 0.059027 | 0.09 |
| 7 | 2 | 3 | -0.046314 | 0.05 |
上の計算結果は、各変数間に直接・間接問わず因果効果が発生した確率とその強さ(総合効果)を表しています。例えば結果の下から2行目は、インデックス3から2(\(x_4 \to x_3\)に対応)へ非零の総合効果が発生した割合がわずか9%であり、発生した総合効果の中央値が0.059027であったことを意味しています。
総合効果の発生している変数の組について、総合効果を発生させている経路のリストは下のようにして可視化することが可能です:
# 因果グラフにおけるfrom_index -> to_indexへの経路pathが確率probabilityで現れ、その総合効果の中央値はeffectである
pd.DataFrame(bs_result.get_paths(from_index=1, to_index=2))
| path | effect | probability | |
|---|---|---|---|
| 0 | [1, 0, 2] | -1.006469 | 1.00 |
| 1 | [1, 2] | 1.942938 | 1.00 |
| 2 | [1, 3, 2] | 0.026794 | 0.27 |
| 3 | [1, 3, 0, 2] | -0.061806 | 0.11 |
| 4 | [1, 0, 3, 2] | 0.000966 | 0.02 |
上の計算結果は、インデックス1から2(\(x_2 \to x_3\)に対応)への経路の発生確率、言うなれば総合効果の内訳を表しています。例えば結果の一番上の行は、インデックス1→0→2(\(x_2 \to x_1 \to x_3\)に対応)のパスが100%の確率で発生しており、その経路で発生した間接効果の中央値が-1.006469であったことを意味します。
以上が、ブートストラップ法による信頼度評価のlingamライブラリにおける実行例です。ここでは簡単な使い方の紹介にとどめましたが、lingamライブラリではほかにも
辺の出現確率を重みとする因果グラフの隣接行列の計算
辺の出現数のカウント時に重みの正負で別の辺とみなすオプション
絶対値が閾値以下の辺や総合効果を無視するオプション
などが利用できます。より詳細な使い方についてはBootstrapResultのAPI Referenceをご参照ください。
ノイズの独立性検定#
LiNGAMではノイズが独立であることや、正規分布に従わないことを仮定していました。lingamライブラリには、その中のノイズの独立性を確認する機能があります。
get_error_independence_p_valuesメソッドでは\(x_i, x_j\)のノイズ\(e_i, e_j\)間の独立性をHSIC testで検定し、そのp値を第\((i,j)\)成分に持つ行列を計算します。HSIC testの帰無仮説は「\(x_i\)のノイズ\(e_i\)と\(x_j\)のノイズ\(e_j\)が独立である」ことですので、第\((i,j)\)成分が有意水準を下回れば\(e_i, e_j\)が従属になってしまっているという判定になります。HSIC testについてより詳しく知りたい方は、Hilbert-Schnidt独立性基準(HSIC)もご参照ください。
l.get_error_independence_p_values(X)
array([[0. , 0.6709759 , 0.09786865, 0.12648566],
[0.6709759 , 0. , 0.79871597, 0.68238392],
[0.09786865, 0.79871597, 0. , 0.2393351 ],
[0.12648566, 0.68238392, 0.2393351 , 0. ]])
例えば有意水準を\(\alpha=0.05\)とすると、今回の例ではすべての非対角成分が\(\alpha\)を上回っているので、どの2変数も「ノイズが従属とは言えない」、という結果になっています。なお、実行結果で対角成分がすべて0になっていますが、対角成分は「\(e_i\)と\(e_i\)自身が独立である」という帰無仮説についての検定のp値ですので0になっても問題ありません。
このノイズの独立性検定の活用方法として、「未観測の共通原因の存在を怪しむ手掛かりにする」というものが挙げられます。例えば先ほどの人工データで\(x_2\)が未観測、すなわちデータに含まれていないとすると
となります。すると\(x_1, x_3, x_4\)のノイズ\(e_1 + e_2, 2 e_2 + e_3, e_2 + e_4\)は互いに独立ではないため、\(x_1, x_3, x_4\)はもはやLiNGAMの仮定には従わなくなってしまいます。そのような状況でDirectLiNGAMによる推定とノイズの独立性検定を行うと、以下の結果になります:
# 未観測共通原因の存在下での推定・ノイズの独立性検定
l_missing = lingam.DirectLiNGAM()
l_missing.fit(X[['$x_1$', '$x_3$', '$x_4$']])
print(l_missing.get_error_independence_p_values(X[['$x_1$', '$x_3$', '$x_4$']]))
[[0.00000000e+00 1.63613492e-08 7.29193225e-01]
[1.63613492e-08 0.00000000e+00 8.78985432e-01]
[7.29193225e-01 8.78985432e-01 0.00000000e+00]]
ノイズの独立性検定の結果を見ると第\((1,2)\)成分が有意水準を大きく下回っているので、\(x_1, x_3\)のノイズが従属であることを示唆しています。このことから、「\(x_1, x_3\)両方の原因となる未観測の変数が背後にあるのではないか?」という可能性を見ることができます。この例では実際、未観測とした\(x_2\)が\(x_1, x_3\)両方の未観測共通原因となっています。
このように、ノイズの独立性検定の結果として未観測共通原因の存在が疑われる場合は、未観測共通原因となる変数のデータを追加して再度分析を行うのがよいでしょう。それが不可能、あるいはそれでも解決しなければDirectLiNGAM以外の手法を利用するのも手です。例えばlingamライブラリにも実装されているRCDはLiNGAMを未観測共通原因ありの場合に拡張した手法で、未観測共通原因が存在する場合にも利用可能です。RCDの使用法についてはlingamライブラリのRCDチュートリアルをご参照ください。
ノイズの正規性検定#
続いて、ノイズの非正規性の仮定を確認してみます。
ここでは正規性検定の一つであるShapiro-Wilk検定を用いて、残差が正規分布に従うかどうかを判定してみます。Shapiro-Wilk検定の帰無仮説は「確率変数が正規分布に従うこと」ですので、p値が有意水準\(\alpha\)(ここでは\(\alpha=0.05\)とする)を下回れば帰無仮説が棄却され、確率変数が正規分布に従わないと判断できます。
# 残差に対する正規性検定(Shapiro-Wilk検定)
# 残差を計算
X_c = X.values - X.values.mean(axis=0)
E = X_c - (l.adjacency_matrix_ @ X_c.T).T
# 可視化
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
fig.suptitle('Shapiro-Wilk tests for residuals')
for i, (col, ax) in enumerate(zip(X.columns, axes)):
ei = E[:, i]
ax.set_title(f'residual of {col} (p-value: {stats.shapiro(ei)[1]:.4f})') # Shapiro-Wilk検定のp値をタイトルに表示
ax.set_ylabel('density')
ax.hist(ei, bins='stone', density=True, alpha=0.3) # ヒストグラムの描画
xlim = ax.get_xlim()
x_pdf = np.linspace(xlim[0], xlim[1], 1000)
ax.plot(x_pdf, stats.norm.pdf(x_pdf, loc=ei.mean(), scale=ei.std()), c='r') # 正規分布の密度関数の描画
fig.show()
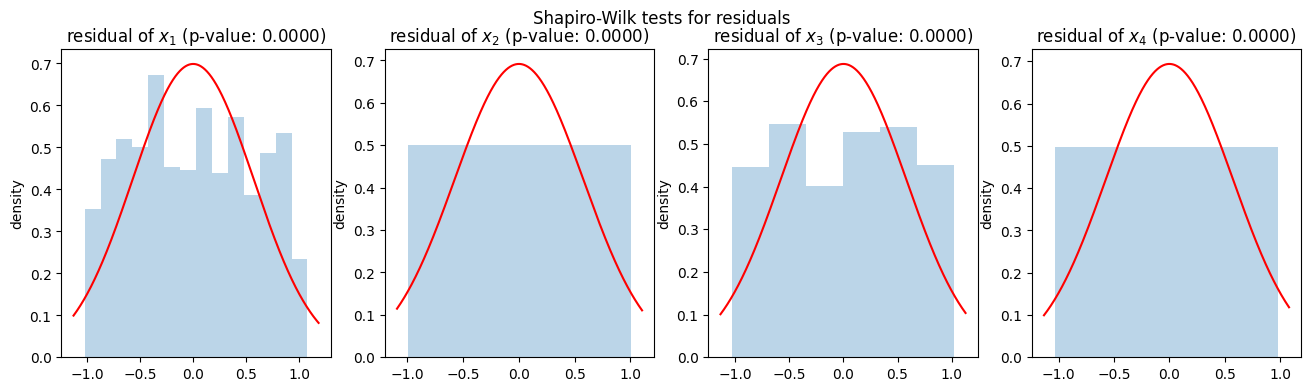
上図のグラフは、各変数の残差\(e_1, e_2, e_3, e_4\)のヒストグラムと正規分布の密度関数を重ねてプロットしたものです。グラフタイトルにあるShapiro-Wilk検定のp値を見ると、\(e_1, e_2, e_3, e_4\)のすべてについて正規性検定のp値がほぼ\(0\)となっています。また、ヒストグラムを見ると残差の分布が正規分布の密度関数とは乖離していることが見て取れます。
この結果から、このデータではノイズがいずれも正規分布には従わない、すなわちLiNGAMにおけるノイズの非正規性の仮定が満たされていることが示唆されます。実際、このデータのノイズは一様分布に従っており、正規分布には従っていません。
小括#
本稿では、DirectLiNGAMの前処理や推定結果の信頼度評価など、DirectLiNGAMのより進んだ内容について解説を行いました。実データに対してDirectLiNGAMを適用する際はぜひ、本稿で解説した信頼度評価なども合わせて行ってみてください。
参考文献#
付録:事前知識の利用#
実データでは各変数の持つ意味合いやドメイン知識から「変数Aと変数Bは直接関係しない」、「変数Cは変数Dの原因である」のように部分的な因果関係が事前知識として分かっているケースがあります。DirectLiNGAMでは、そのような事前知識を利用するアルゴリズムがあります。
事前知識を利用すると
事前知識と矛盾しない推定結果が得られるので推定精度の向上が見込める
事前知識を用いて外生変数の探索候補を減らせるので計算時間の短縮が期待できる
などさまざまなメリットがあります。
lingamライブラリにも事前知識を利用するアルゴリズムが実装されており、lingam.DirectLiNGAMのインスタンス生成時に事前知識行列を指定することで事前知識ありのアルゴリズムで推定が行われます。
ここで、事前知識行列\(\mathbf{A}^\text{knw}\)とは\(0, 1, -1\)のいずれかを成分とする\(d \times d\)行列(ただし\(d\)は特徴量の個数)であり、その第\((i,j)\)成分\(a_{ij}^\text{knw}\)の値がそれぞれ以下の事前知識に対応するものです:
例えば特徴量\(x_1, x_2, x_3, x_4\)について「\(x_2 \to x_3\)の因果関係があることだけ知っているがそれ以外は何も分からない」という事前知識を表す事前知識行列は
となります。ちなみに、この例では因果グラフは非巡回であるという仮定から「辺\(x_3 \to x_2\)は存在しない」・「辺\(x_i \to x_i\)は存在しない(\(i=1,2,3,4\))」ということも分かるのでそれを加味した事前知識行列にしても大丈夫です。
では実際に事前知識ありのDirectLiNGAMで推定を行ってみましょう。今回は本文中で使用したのと同じ人工データに対して、\(x_2 \to x_3\)の因果関係があることだけ知っているがそれ以外は何も分からない」という事前知識を与えた上でDirectLiNGAMによる推定を行ってみます。
# 事前知識行列Aknwの定義
Aknw = np.array([
[-1, -1, -1, -1],
[-1, -1, -1, -1],
[-1, 1, -1, -1],
[-1, -1, -1, -1],
])
# 事前知識ありDirectLiNGAMによる推定
l_knw = lingam.DirectLiNGAM(prior_knowledge=Aknw)
l_knw.fit(X)
# ここから推定結果の可視化を行う
fig_a, axes_a = plt.subplots(1, 2, figsize=(10, 5))
# 推定結果のグラフ描画
G = nx.from_numpy_array(l_knw.adjacency_matrix_.T, create_using=nx.DiGraph())
G = nx.relabel_nodes(G, {v: fr'$x_{i+1}$' for i, v in enumerate(G.nodes())})
e_label_dict_est = {(i, j): f'{d["weight"]:.4f}' for i, j, d in G.edges(data=True)}
e_width_list_est = [ abs(d['weight']) for (u, v, d) in G.edges(data=True)]
axes_a[0].set_title(f'DirectLiNGAM with prior knowledge')
nx.draw_networkx_nodes(G, pos, ax=axes_a[0], node_size=600, node_color='#ffaaaa', edgecolors='k')
nx.draw_networkx_edges(G, pos, ax=axes_a[0], width=e_width_list_est, style='solid', arrowstyle='->', node_size=600, arrowsize=20)
nx.draw_networkx_labels(G, pos, ax=axes_a[0])
nx.draw_networkx_edge_labels(G, pos, edge_labels=e_label_dict_est, ax=axes_a[0], rotate=False)
axes_a[1].set_title(f'True')
nx.draw_networkx_nodes(Gtrue, pos, ax=axes_a[1], node_size=600, node_color='#ffaaaa', edgecolors='k')
nx.draw_networkx_edges(Gtrue, pos, ax=axes_a[1], width=e_width_list_true, style='solid', arrowstyle='->', node_size=600, arrowsize=20)
nx.draw_networkx_labels(Gtrue, pos, ax=axes_a[1])
nx.draw_networkx_edge_labels(Gtrue, pos, edge_labels=e_label_dict_true, ax=axes_a[1], rotate=False)
fig_a.show()
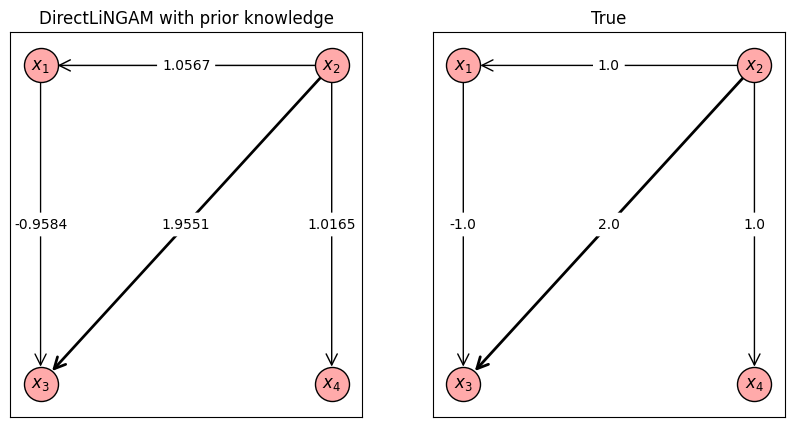
上図は事前知識ありDirectLiNGAMの推定結果と真の因果グラフを並べたものです。今回の人工データはLiNGAMによる因果探索(基本編)の実行例にもあるように事前知識を使わずともすでに高い精度で推定ができていたので、上の計算例では事前知識を利用することによる精度向上のメリットはあまり見せられていませんが、DirectLiNGAMを使った分析をする際はここで紹介した事前知識の利用も検討してもらえると幸いです。
また、事前知識ありDirectLiNGAMでも本文中で紹介した信頼度評価(ブートストラップ法・ノイズの独立性検定・ノイズの正規性検定)は同様のコードで実行できますので、これらも合わせてご活用ください。

