一般化線形モデルの基礎

このページでは、 一般化線形モデル (generalized linear model; GLM) と呼ばれる確率モデルの概要を解説します。一般化線形モデルとはその名の通り線形回帰モデルを拡張（一般化）したモデルのことで、その中には

• ポアソン回帰モデル (Poisson regression model)

• ガンマ回帰モデル (gamma regression model)

などのモデルが含まれます。これらのモデルを用いることで、

• 0以上の整数値（ \(0, 1, 2, \ldots\) ）のみを取る変数（カウントデータなど）や

• 0以上の値のみを取る変数（待ち時間や製品の寿命など）

を目的変数とする場合でも統計的に自然な設定で分析を行うことが可能になります。これら個別のモデルについての解説と具体的な分析例は別のページで解説予定です。

また、同じく一般化線形モデルの一種であるロジスティック回帰モデル (logistic regression model) についても別のページで解説しています。

一般化線形モデルの動機付け

「一般化」線形モデルのことを考える前に、その元となった線形回帰モデルのことを少し変わった視点から振り返ってみましょう。

説明変数（入力変数） \(\mathbf{x}_i = ( x_{i, 1}, \ldots, x_{i, K} ) = ( x_{i, k} )_{k = 1}^K \in \mathbf{R}^K\) と目的変数（出力変数） \(y_i \in \mathbf{R}\) の関係を学習したいものとします。このときよく使われる単純なモデルが 線形回帰モデル (linear regression model) で、これらの変数の間に

\[ y_i = b_0 + \sum_{k = 1}^K b_k x_{i, k} + \epsilon_i \]

という線形結合の関係を仮定します。ここで \(\epsilon_i \in \mathbf{R}\) は分散 \(\sigma^2 > 0\) の正規分布 \(\mathrm{N} (0, \sigma^2)\) に従う雑音 (noise) で、 \(\mathbf{b} = ( b_0, b_1, \ldots, b_K ) = ( b_k )_{k = 0}^K \in \mathbf{R}^{K + 1}\) はこのモデルのパラメータ（切片と回帰係数）です。

線形回帰モデルの学習では、与えられた訓練データ \(D = ( \mathbf{x}_i, y_i )_{i = 1}^N\) を用いて最小二乗法や最尤推定などの方法でパラメータ \(\mathbf{b} \in \mathbf{R}^{K + 1}\) の推定値 \(\hat{\mathbf{b}} = ( \hat{b}_k )_{k = 0}^K = \in \mathbf{R}^{K + 1} \) を計算します。多くの場合、この推定値 \(\mathbf{b}\) の計算の過程で雑音の分散 \(\sigma^2\) は陽に現れないため、この \(\sigma^2\) の具体的な値のことを忘れたまま \(\hat{\mathbf{b}}\) の値を決定することができます。

さて、この線形回帰モデルの別の表現を考えてみます。説明変数 \(\mathbf{x}_i = ( x_{i, k} )_{k = 1}^K\) の線型結合

\[ \eta_i = b_0 + \sum_{k = 1}^K b_k x_{i, k} \]

を用いると、線形回帰モデルで目的変数 \(y_i\) の従う分布は平均 \(\mu_i = \eta_i\) 、分散 \(\sigma^2 > 0\) の正規分布 \(\mathrm{N} ( \mu_i, \sigma^2 )\) として表すことができます。正規分布の性質から明らかなように、 \(\mu_i\) = \(\eta_i\) は目的変数 \(y_i\) の（条件付き）期待値になっています。

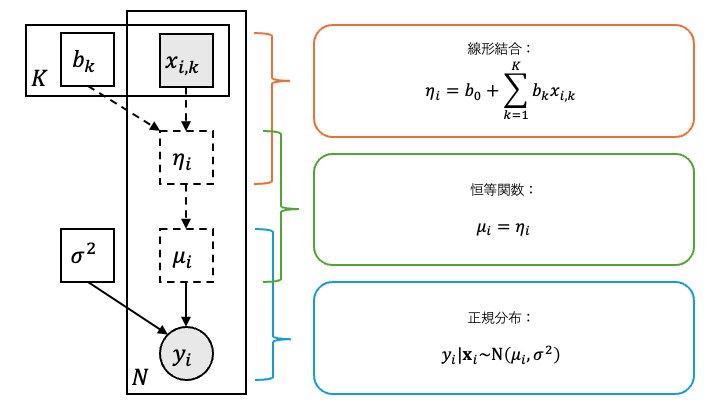
即ち、線形回帰モデルとは

• 目的変数 \(y_i\) が従う（条件付き）確率分布を正規分布 \(\mathrm{N} ( \mu_i, \sigma^2 )\) と仮定した上で、

• 目的変数 \(y_i\) の（条件付き）期待値 \(\mu_i\) を説明変数の線形結合 \(\eta_i\) の関数（恒等関数）で表現した

モデルだと思うことができます。また、線形回帰モデルでは目的変数 \(y_i\) の統計的な性質として

• 目的変数 \(y_i\) が潜在的に実数 \(\mathbf{R}\) の全域 \(( - \infty, \infty )\) に値を取りうることと、

• 目的変数 \(y_i\) の値の統計的なばらつきが \(\mathbf{x}_i\) や \(y_i\) の値によらず一定（分散 \(\sigma^2\) ）であること

を仮定していることになります。

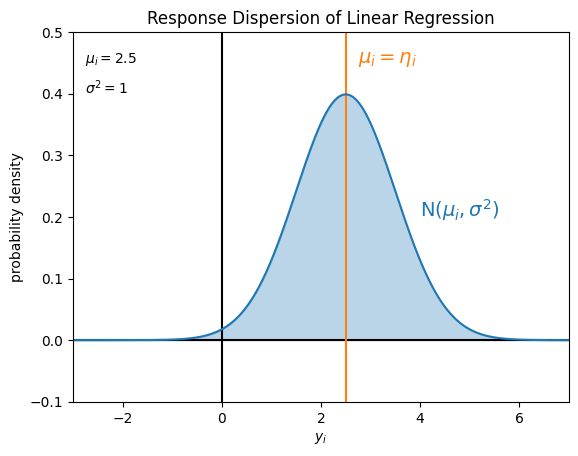
線形回帰モデルが仮定している目的変数 \(y_i\) の値のばらつきは、例えば次の図のようになります。

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

Show code cell source Hide code cell source

_xlim = (-3, 7)
_ylim = (-0.1, 0.5)

_mu = 2.5
_sigma = 1
_x = np.arange(*_xlim, 0.01)
_f = stats.norm.pdf(_x, loc=_mu, scale=_sigma)

fig, ax = plt.subplots(1)
ax.set_title("Response Dispersion of Linear Regression")
ax.set_xlim(*_xlim)
ax.set_ylim(*_ylim)
ax.set_xlabel("$y_i$")
ax.set_ylabel("probability density")
ax.hlines(0.0, *_xlim, colors="black")
ax.vlines(0.0, *_ylim, colors="black")
ax.vlines(_mu, *_ylim, colors="C1")
ax.plot(_x, _f, label="$\\mu_i = \\eta_i$", color="C0")
ax.fill_between(_x, _f, color="C0", alpha=0.3)
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.05, f"$\\mu_i = {_mu}$")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.1, f"$\\sigma^2 = {_sigma ** 2}$")
ax.text(_mu + 0.25, _ylim[1] - 0.05, "$\\mu_i = \\eta_i$", color="C1", fontsize=14)
ax.text(4, 0.2, "$\\mathrm{N} ( \\mu_i, \\sigma^2 )$", color="C0", fontsize=14)

plt.show()

ところで、実際のデータ分析では、考えている目的変数 \(y_i\) の値域 \(\mathcal{Y}\) が実数 \(\mathbf{R}\) の全域 \(( - \infty, \infty )\) より真に小さいことがあります。例えば

• \(y_i\) は0以上の整数値のみを取る（ \(\mathcal{Y} = \{ 0, 1, 2, \ldots \}\) ）、ないし

• \(y_i\) は0以上の値のみを取る（ \(\mathcal{Y} = [0, \infty)\) ）

といったような場合です。例えば目的変数 \(y_i\) がカウントデータ（計数データ）である場合には前者の（非負の整数値のみという）仮定を置くことが自然です。また、目的変数 \(y_i\) の統計的なばらつきについても \(\mathbf{x}_i\) や \(y_i\) の値に依存して何らかの傾向があることは珍しくありません。

これらの場合に線形回帰モデルをそのまま当てはめてしまうと、モデルの予測値が説明変数 \(\mathbf{x}_i\) の値次第で不適切な範囲の値（カウントデータに対して負の値など）を取ってしまったり、目的変数の統計的なばらつきと整合しない不適切な値を指してしまったりすることがあります。そこで、一般化線形モデルでは

• 目的変数 \(y_i\) が従う（条件付き）確率分布を正規分布以外の分布にも拡張しつつ、

• 目的変数 \(y_i\) の（条件付き）期待値 \(\mu_i\) を説明変数の線形結合 \(\eta_i\) の関数として表現する

という形でこれらのさまざまな値域 \(\mathcal{Y}\) や想定される統計的なばらつきに対応するモデルを定義し、統計的推論や学習を行っていくことになるのです。

一般化線形モデルの定義と具体例

この節では、一般化線形モデルの定義について述べた後、その中に含まれるモデルの具体例やPythonにおける取り扱いを説明します。

一般化線形モデルの定義

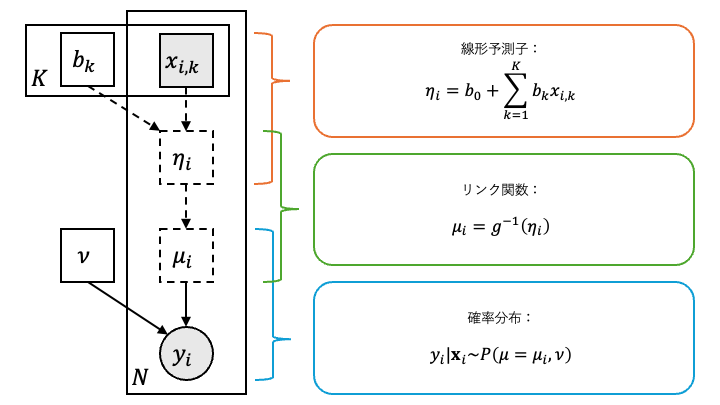
一般化線形モデルでは、説明変数 \(\mathbf{x}_i = ( x_{i, k} )_{k = 1}^K \in \mathbf{R}^K\) と目的変数 \(y_i \in \mathcal{Y} \subseteq \mathrm{R}\) の関係を記述するために次の3つの要素

• 確率分布 \(P ( \mu )\)

• リンク関数 (link function) \(g ( \mu ) = \eta\)

• 線形予測子 (linear predictor) \(\eta_i = b_0 + \sum_{k = 1}^K b_k x_{i, k}\)

を用います。ただし \(\mu \in \mathbf{R}\) は確率分布 \(P\) の期待値にあたるパラメータで、 \(\mathbf{b} = ( b_k )_{k = 0}^K \in \mathbf{R}^{K + 1}\) は線形予測子のパラメータです。

はじめに説明変数 \(\mathbf{x}_i = ( x_{i, k} )_{k = 1}^K\) の値から線形予測子 \(\eta_i = b_0 + \sum_{k = 1}^K b_k x_{i, k}\) の値を計算します。次にリンク関数 \(g\) の逆関数 \(g^{- 1}\) を用いて

\[ \mu_i = g^{- 1} ( \eta_i ) = g^{- 1} \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \]

によって \(\mu_i \in \mathbf{R}\) を定めます。最後にこの \(\mu_i\) を確率分布 \(P\) の期待値パラメータとして、目的変数 \(y_i\) の従う（条件付き）確率分布を \(P ( \mu_i )\) と仮定します。以上をまとめると

\[ y_i | \mathbf{x}_i \sim P \left( \mu = g^{- 1} \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \right) \]

と記述できることになり、これが一般化線形モデルの基本になります。

訓練データ \(D = ( \mathbf{x}_i, y_i )_{i = 1}^N\) が与えられたとき、まず計算するものは線形予測子のパラメータ \(\mathbf{b} \in \mathbf{R}^{K + 1}\) の推定値 \(\hat{\mathbf{b}} = ( \hat{b}_k )_{k = 0}^K \in \mathbf{R}^{K + 1}\) です。もし確率分布 \(P\) が期待値パラメータ \(\mu \in \mathbf{R}\) 以外のパラメータ \(\nu\) を持っている場合でも、多くはその \(\nu\) の具体的な値を忘れたまま \(\hat{\mathbf{b}}\) の値を決定することができます。このため、以降は（も）このような確率分布 \(P ( \mu, \nu )\) を単に \(P ( \mu )\) と書くことにします。

改めて、 \(\mu_i\) は確率分布 \(P ( \mu_i )\) の期待値にあたるパラメータなので、目的変数 \(y_i\) の（条件付き）期待値は

\[ \mathrm{E} [ y_i | \mathbf{x}_i ] = \mu_i = g^{- 1} \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \]

と表すことができます。つまり、機械学習的な文脈ではこの \(\mu_i\) こそが目的変数 \(y_i\) に対応するモデルの「出力」 \(\hat{y}_i\) にほかなりません。

したがって、もしデータから何らかの方法で線形予測子のパラメータ \(\mathbf{b} \in \mathbf{R}^{K + 1}\) の推定値 \(\hat{\mathbf{b}} = ( \hat{b}_k )_{k = 0}^K \in \mathbf{R}^{K + 1}\) が計算できたとすると、新しい入力の説明変数 \(\mathbf{x}_\mathrm{new} = (x_{\mathrm{new}, k})_{k = 1}^K \in \mathbf{R}^K\) に対応する目的変数の予測値 \(\hat{y}_\mathrm{new}\) は

\[ \hat{y}_\mathrm{new} = \hat{\mu}_\mathrm{new} = g^{- 1} \left( \hat{b}_0 + \sum_{k = 1}^K \hat{b}_k x_{\mathrm{new}, k} \right) \]

と表すことができます。

一般化線形モデルで使われる確率分布

通例として、一般化線形モデルに使われる確率分布 \(P\) は指数型分布族 (exponential family) と呼ばれる確率分布のクラス（もしくはその適当な拡張）の中から選ばれます。特に、scikit-learnやstatsmodelsに実装されているような基本的なモデルでは（一変数の） 指数分散モデル (exponential dispersion model; EDM) というクラスの中から \(P\) が選ばれています。指数分散モデルとは

\[ p ( y ; \theta, \phi ) = C ( y, \phi ) \exp \left( \frac{y \theta - A ( \theta )}{\phi} \right) \]

のような形の確率密度関数を持つ確率分布のクラスで、この \(\theta \in \mathbf{R}\) を自然パラメータ (natural parameter) 、 \(\phi > 0\) を分散パラメータ (dispersion parameter) などと呼びます。

指数分散モデルのクラスに属する確率分布としては

• 正規分布 \(\mathrm{N} ( \mu, \sigma^2 )\)

• ポアソン分布 \(\mathrm{Po} ( \lambda )\)

• ガンマ分布 \(\mathrm{Ga} ( \alpha, \beta )\)

• 逆ガウス分布 \(\mathrm{IG} ( \mu, \lambda )\)

• 二項分布 \(\mathrm{B} ( n, p )\)

• 負の二項分布 \(\mathrm{NB} (r, p)\)

• Tweedie分布 \(\mathrm{Tw}_p ( \mu, \phi )\)

などがあります。例えば正規分布 \(\mathrm{N} ( \mu, \sigma^2 )\) の確率密度関数は

\[\begin{split} \begin{align*} p ( y ; \mu, \sigma^2 ) & = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{(y - \mu)^2}{2 \sigma^2} \right) \\ & = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{y^2}{2 \sigma^2} \right) \exp \left( \frac{y \mu - \frac{1}{2} \mu^2}{\sigma^2} \right) \end{align*} \end{split}\]

と変形できるので、自然パラメータ \(\theta = \mu\) 、分散パラメータ \(\phi = \sigma^2\) としてたしかに指数分散モデルに属することが確認できます。

Tweedie分布 \(\mathrm{Tw}_p ( \mu, \phi )\) は指数分散モデルを代表する確率分布です。パワーパラメータ (power parameter) \(p\) の値によって、

• \(p = 0\): 正規分布

• \(p = 1\): （過分散）ポアソン分布

• \(p = 2\): ガンマ分布

• \(p = 3\): 逆ガウス分布

などの分布がこの分布の特殊な場合として表れます。

指数分散モデルの確率分布の中には2つ以上のパラメータを持つものもありますが、基本的にはそのうち1つだけを未知パラメータとして適切に選択します。選択されなかったそれ以外のパラメータは局外パラメータ (nuisance parameter) として、

• 既知のものとして扱うか、

• 一般化線形モデルの枠組みの外で（モデル選択などの手法で）決定するか

などします。これらの局外パラメータは（適切に選択すれば）実際に \(\hat{\mathbf{b}} \in \mathbf{R}^{K + 1}\) の値を求める計算過程で陽に出現しないことも多く、その場合は（線形回帰モデルにおける分散 \(\sigma^2\) のように）具体的な値を忘れたままでも \(\hat{\mathbf{b}}\) の値を決定することができます。実装上の局外パラメータの扱いはライブラリによって異なりますが、特に分散パラメータ \(\phi\) に関連するパラメータは局外パラメータとして扱われることが多く、 \(\hat{\mathbf{b}}\) の値を決定する過程では暗に \(\phi = 1\) と仮定されていることが多々あります。

一般化線形モデルにおいて、目的変数の値域 \(\mathcal{Y}\) ごとによく使われる確率分布 \(P\) 、その期待値パラメータ \(\mu_i\) へのパラメータ変換、リンク関数 \(g\) の組の一覧は下記の表の通りです。

一般化線形モデルの例

値域 \(\mathcal{Y}\)	確率分布 \(P\)	期待値パラメータ \(\mu_i\)	リンク関数 \(g ( \mu_i ) = \eta_i\)	備考
実数の全域 \(( - \infty, \infty )\)	正規分布 \(\mathbf{N} ( \mu_i, \sigma^2 )\)	\(\mu_i\)	\(\mu_i = \eta_i\)	線形回帰モデルと同等
非負の整数 \(\{ 0, 1, 2, \ldots \}\)	ポアソン分布 \(\mathrm{Po} ( \lambda_i )\)	\(\mu_i = \lambda_i\)	\(\log ( \mu_i ) = \eta_i\)	ポアソン回帰モデル
非負の実数 \((0, \infty )\)	ガンマ分布 \(\mathrm{Ga} ( \alpha, \beta_i )\)	\(\mu_i = \frac{\alpha}{\beta_i}\)	\(\log ( \mu_i ) = \eta_i\) または \(- \frac{1}{\mu_i} = \eta_i\)	ガンマ回帰モデル
上限のある非負の整数 \(\{ 0, 1, \ldots, n \}\)	二項分布 \(\mathrm{B} ( n, p_i )\)	\(\mu_i = n p_i\)	\(\log \left( \frac{\mu_i}{1 - \mu_i} \right) = \eta_i\)	ロジスティック回帰モデルと同等

ただし、これらの確率分布 \(P\) の（一般的な）パラメータのうち上記の表の中で添字 \(i\) を付していないもの、すなわち

• 正規分布の分散 (variance) \(\sigma^2\)

• ガンマ分布の形状 (scale) パラメータ \(\alpha\)

• 二項分布の試行回数 \(n\)

については局外パラメータとして扱います（即ち、既知のものとして扱うか一般化線形モデルの枠組みの外で決定するものとします）。

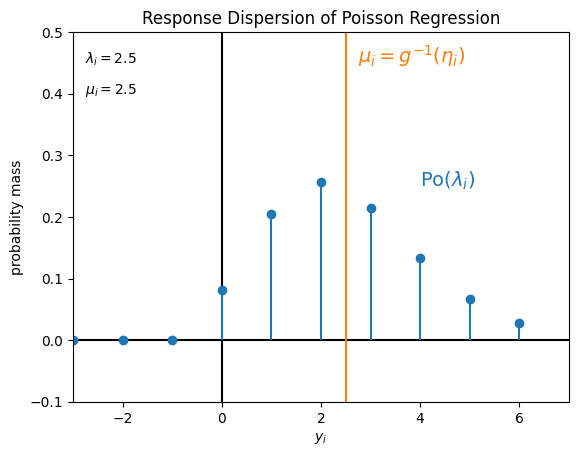
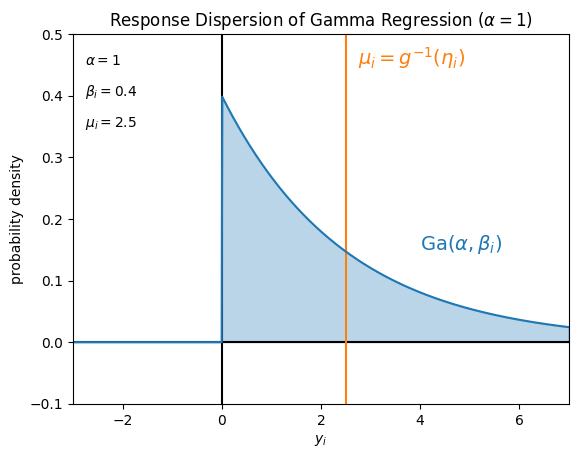
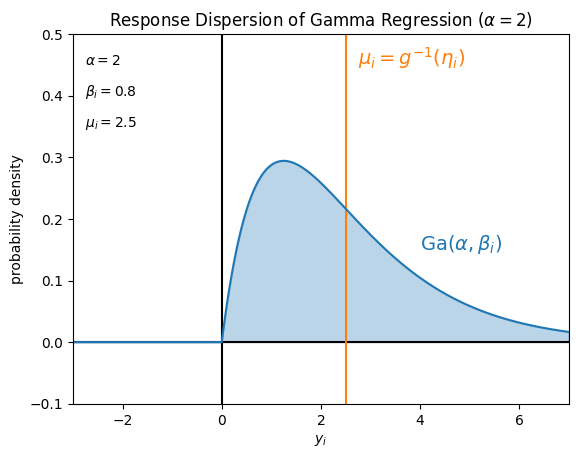
一例として、確率分布 \(P\) を

• ポアソン分布 \(\mathrm{Po} (\lambda_i)\)

• ガンマ分布 \(\mathrm{Ga} (\alpha = 1, \beta_i)\)

• ガンマ分布 \(\mathrm{Ga} (\alpha = 2, \beta_i)\)

とした場合に仮定している目的変数 \(y_i\) の値のばらつきは、例えばそれぞれ次の図のようになります。

Show code cell source Hide code cell source

_xlim = (-3, 7)
_ylim = (-0.1, 0.5)

_mu = 2.5
_x = np.arange(*_xlim, 0.01)
_k = np.arange(*_xlim, 1)
_f = stats.poisson.pmf(_k, mu=_mu)

fig, ax = plt.subplots(1)
ax.set_title("Response Dispersion of Poisson Regression")
ax.set_xlim(*_xlim)
ax.set_ylim(*_ylim)
ax.set_xlabel("$y_i$")
ax.set_ylabel("probability mass")
ax.hlines(0.0, *_xlim, colors="black")
ax.vlines(0.0, *_ylim, colors="black")
ax.vlines(_mu, *_ylim, colors="C1")
ax.stem(_k, _f, linefmt="C0", markerfmt="C0", basefmt=" ")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.05, f"$\\lambda_i = {_mu}$")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.1, f"$\\mu_i = {_mu}$")
ax.text(
    _mu + 0.25,
    _ylim[1] - 0.05,
    "$\\mu_i = g^{-1} ( \\eta_i )$",
    color="C1",
    fontsize=14,
)
ax.text(4, 0.25, "$\\mathrm{Po} ( \\lambda_i )$", color="C0", fontsize=14)

plt.show()

Show code cell source Hide code cell source

_xlim = (-3, 7)
_ylim = (-0.1, 0.5)

_mu = 2.5
_alpha = 1
_beta = _alpha / _mu
_x = np.arange(*_xlim, 0.01)
_f = stats.gamma.pdf(_x, a=_alpha, scale=1.0 / _beta)

fig, ax = plt.subplots(1)
ax.set_title(f"Response Dispersion of Gamma Regression ($\\alpha = {_alpha}$)")
ax.set_xlim(*_xlim)
ax.set_ylim(*_ylim)
ax.set_xlabel("$y_i$")
ax.set_ylabel("probability density")
ax.hlines(0.0, *_xlim, colors="black")
ax.vlines(0.0, *_ylim, colors="black")
ax.vlines(_mu, *_ylim, colors="C1")
ax.plot(_x, _f, color="C0")
ax.fill_between(_x, _f, color="C0", alpha=0.3)
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.05, f"$\\alpha = {_alpha}$")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.1, f"$\\beta_i = {_beta}$")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.15, f"$\\mu_i = {_mu}$")
ax.text(
    _mu + 0.25,
    _ylim[1] - 0.05,
    "$\\mu_i = g^{-1} ( \\eta_i )$",
    color="C1",
    fontsize=14,
)
ax.text(4, 0.15, "$\\mathrm{Ga} ( \\alpha, \\beta_i )$", color="C0", fontsize=14)

plt.show()

Show code cell source Hide code cell source

_xlim = (-3, 7)
_ylim = (-0.1, 0.5)

_mu = 2.5
_alpha = 2
_beta = _alpha / _mu
_x = np.arange(*_xlim, 0.01)
_f = stats.gamma.pdf(_x, a=_alpha, scale=1.0 / _beta)

fig, ax = plt.subplots(1)
ax.set_title(f"Response Dispersion of Gamma Regression ($\\alpha = {_alpha}$)")
ax.set_xlim(*_xlim)
ax.set_ylim(*_ylim)
ax.set_xlabel("$y_i$")
ax.set_ylabel("probability density")
ax.hlines(0.0, *_xlim, colors="black")
ax.vlines(0.0, *_ylim, colors="black")
ax.vlines(_mu, *_ylim, colors="C1")
ax.plot(_x, _f, color="C0")
ax.fill_between(_x, _f, color="C0", alpha=0.3)
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.05, f"$\\alpha = {_alpha}$")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.1, f"$\\beta_i = {_beta}$")
ax.text(_xlim[0] + 0.25, _ylim[1] - 0.15, f"$\\mu_i = {_mu}$")
ax.text(
    _mu + 0.25,
    _ylim[1] - 0.05,
    "$\\mu_i = g^{-1} ( \\eta_i )$",
    color="C1",
    fontsize=14,
)
ax.text(4, 0.15, "$\\mathrm{Ga} ( \\alpha, \\beta_i )$", color="C0", fontsize=14)

plt.show()

Pythonでの取り扱い

Pythonで一般化線形モデルを用いた推論を行う場合、statsmodelsやscikit-learnなどの汎用ライブラリを利用することができます。ここではそれぞれのライブラリにおける一般化線形モデルに関するクラスや関数を簡単に紹介していきます。

statsmodelsでは

• sm.GLM クラスや

• smf.glm() 関数

を用いると多様な一般化線形モデルを利用することができます。どちらを用いる場合も、使用する確率分布 \(P\) は引数 family で（所定の分布の中から選択して）指定します。また、目的変数が離散値となる回帰モデルについては

• sm.Logit （ロジスティック回帰モデル）や

• sm.Poisson （ポアソン回帰モデル）

など個別のクラスが用意されているものがあります。

import statsmodels.api as sm

print(sm.GLM.__doc__.splitlines()[1])  # 一般化線形モデル全般に対応するクラス

    Generalized Linear Models

print(sm.Poisson.__doc__.splitlines()[1])  # ポアソン回帰モデルに対応するクラス

    Poisson Model

scikit-learnでは

• linear_model.TweedieRegressor クラス

でTweedie分布を使用した一般化線形モデルが提供されています。この際、引数 power でTweedie分布のパワーパラメータ \(p\) を指定します。また、このクラスのラッパーとして

• linear_model.PoissonRegressor クラス（ポアソン回帰モデル）と

• linear_model.GammaRegressor クラス（ガンマ回帰モデル）

も提供されています。なお、ロジスティック回帰モデルにつていは linear_model.LogisticRegression クラスで分類モデルとして提供されています。

from sklearn.linear_model import TweedieRegressor, PoissonRegressor

print(TweedieRegressor.__doc__.splitlines()[0])  # Tweedie回帰モデルに対応するクラス

Generalized Linear Model with a Tweedie distribution.

print(PoissonRegressor.__doc__.splitlines()[0])  # ポアソン回帰モデルに対応するクラス

Generalized Linear Model with a Poisson distribution.

一般化線形モデルの推定と評価

この節では、一般化線形モデルの推定・評価方法とその中で用いる「逸脱度」の概念について説明した後、それらのPythonにおける取り扱いを確認します。

一般化線形モデルの推定

一般化線形モデルを仮定した際に、まず推定すべきものは線形予測子のパラメータ \(\mathbf{b} = (b_0, b_1, \ldots, b_K) \in \mathbf{R}^{K+1}\) です。

一般化線形モデルの最尤推定

統計的な文脈で、線形予測子のパラメータ \(\mathbf{b}\) の最尤推定の方法を考えていきます。一般化線形モデルにおいて \(\mathbf{b}\) はモデル中の確率分布 \(P ( \mu_i )\) の期待値パラメータ \(\mu_i\) を通じてのみ確率密度関数の値に影響するので、このことを

\[ \mu_i = \mu_i ( \mathbf{b} ) = g^{- 1} \left( b_0 + \sum_{k = 1}^K b_k x_{i, k} \right) \]

と表現することにします。いま、確率分布 \(P ( \mu )\) の確率密度関数を \(p ( y; \mu )\) とおくと、訓練データ \(D = ( \mathbf{x}_i, y_i )_{i = 1}^N\) が与えられたときの対数尤度 \(\ell ( \mathbf{b}; D)\) は

\[\begin{split} \begin{align*} \ell ( \mathbf{b}; D ) & = \log \left( \prod_{i = 1}^N p ( y_i ; \mu = \mu_i ( \mathbf{b} ) ) \right) \\ & = \sum_{i = 1}^N \log p ( y_i ; \mu = \mu_i ( \mathbf{b} ) ) \end{align*} \end{split}\]

となります。あとはこれを \(\mathbf{b}\) について（数値的に）最大化して

\[ \hat{\mathbf{b}}_\mathrm{MLE} = \arg \max_\mathbf{b} \ell ( \mathbf{b}; D ) \]

とすれば最尤推定量 \(\hat{\mathbf{b}}_\mathrm{MLE}\) を求めることができます。

一般化線形モデルの逸脱度による推定

一方で、 逸脱度 (deviance) の概念から線形予測子のパラメータ \(\mathbf{b}\) を決定することもできます。逸脱度とはモデルの当てはまりの良さ (goodness of fit) を測る指標の一つで、 飽和モデル (saturated model) と呼ばれる自明なモデルの対数尤度と比べてモデルの対数尤度 \(\ell ( \mathbf{b}; D )\) がどれほど小さいか（悪いか）を示すものです。

一般化線形モデルに対する飽和モデルとは、訓練データのサイズと同じ \(N\) 個のパラメータを用いて元のモデルと同じ確率分布 \(P\) が訓練データの目的変数の値 \(( y_i )_{i = 1}^N\) にうまく当てはまるようにしたモデルのことを指します。具体的には、訓練データと完全に同じ値の \(N\) 個のパラメータ \(y_1, \ldots, y_N \in \mathcal{Y} \subseteq \mathbf{R}\) を用いて

\[ y_i | \mathbf{x}_i \sim P ( \mu = y_i ) \]

となるようにした（自明な）モデルのことです。この飽和モデルにおいて、訓練データにおける \(y_i\) の（条件付き）期待値（すなわち、モデルの「出力」 \(\hat{y}_i\) ）は目的変数の値 \(y_i\) と完全に一致します。これが一般化線形モデルに対する飽和モデルで、文献によっては フルモデル (full model) とも呼ばれます。

この飽和モデルを用いたときのデータの対数尤度 \(\ell_\mathrm{s} (D)\) は

\[\begin{split} \begin{align*} \ell_\mathrm{s} ( D ) & = \log \left( \prod_{i = 1}^N p ( y_i ; \mu = y_i ) \right) \\ & = \sum_{i = 1}^N \log p ( y_i ; \mu = y_i ) \end{align*} \end{split}\]

と表せます。この \(\ell_\mathrm{s} ( D )\) は、訓練データ \(D\) への当てはめという意味で最善の一般化線形モデルが達成する対数尤度の値と思うことができます。

一般化線形モデルにおける逸脱度 \(\mathrm{Dev} ( \mathbf{y} , \boldsymbol{\mu} ( \mathbf{b} ) )\) は、この2つの対数尤度 \(\ell ( \mathbf{b}, D )\) と \(\ell_\mathrm{s} ( D )\) を用いて

\[\begin{split} \begin{align*} \mathrm{Dev} ( \mathbf{y} , \boldsymbol{\mu} ( \mathbf{b} ) ) & = 2 ( \ell_\mathrm{s} ( D ) - \ell ( \mathbf{b}, D ) ) \\ & = 2 \left( \sum_{i = 1}^N \log p ( y_i ; \mu = y_i ) - \sum_{i = 1}^N \log p ( y_i ; \mu = \mu_i ( \mathbf{b} ) ) \right) \end{align*} \end{split}\]

として定義されます。ただし、 \(\mathbf{y} = ( y_i )_{i=1}^N\) および \(\boldsymbol{\mu} ( \mathbf{b} ) = ( \mu_i ( \mathbf{b} ) )_{i = 1}^N\) とおきました。この定義による「逸脱度」は文献によっては 残差逸脱度 (residual deviance) とも呼ばれています。

この逸脱度は

\[ \mathrm{Dev} ( \mathbf{y} , \boldsymbol{\mu} ( \mathbf{b} ) ) = \sum_{i = 1}^N 2 ( \log p ( y_i ; \mu = y_i ) - \log p ( y_i ; \mu = \mu_i ( \mathbf{b} ) ) ) \]

とも表せるので、総和記号の中の各項

\[ d ( y_i, \mu_i ( \mathbf{b} ) ) = 2 ( \log p ( y_i ; \mu = y_i ) - \log p ( y_i ; \mu = \mu_i ( \mathbf{b} ) ) ) \]

を訓練データ \(D\) の各点 \(( \mathbf{x}_i, y_i )\) に対応する逸脱度と思うことができます。この \(d ( y_i, \mu_i ( \mathbf{b} ) )\) は、対応する一般化線形モデルの unit deviance と呼ばれます。なお、文献や実装によっては分散パラメータ \(\phi = 1\) のときの \(d ( y_i, \mu_i ( \mathbf{b} ) )\) を単に「unit deviance」と呼んでいることもあります。

このunit devianceには

• モデルの出力が「正解」 \(\mu_i( \mathbf{b} ) = y_i\) だったとき \(d ( y_i, \mu_i ( \mathbf{b} ) ) = 0\) となる、

• 確率分布 \(P\) が正規分布 \(\mathbf{N} ( \mu, 1 )\) のとき、 \(d ( y_i, \mu_i ( \mathbf{b} ) ) = ( y_i - \mu_i ( \mathbf{b} ) )^2\) となる

などの性質があるため、二乗誤差の概念を正規分布以外の指数分散モデルの分布にも拡張したものと見なすことがあります。したがって、その平均を最小にする

\[ \hat{\mathbf{b}}_\mathrm{D} = \arg \min_\mathbf{b} \frac{1}{N} \sum_{i = 1}^N d ( y_i, \mu_i ( \mathbf{b} ) ) \]

を線形予測子のパラメータ \(\mathbf{b}\) のパラメータの推定量とすることにします。

なお、この推定量 \(\hat{\mathbf{b}}_\mathrm{D}\) は

\[\begin{split} \begin{align*} \hat{\mathbf{b}}_\mathrm{D} & = \arg \min_\mathbf{b} \frac{1}{N} \mathrm{Dev} ( \mathbf{y} , \boldsymbol{\mu} ( \mathbf{b} ) ) \\ & = \arg \min_\mathbf{b} \frac{1}{N} ( \ell_\mathrm{s} ( D ) - \ell ( \mathbf{b}, D ) ) \\ & = \arg \max_\mathbf{b} \ell ( \mathbf{b}, D ) \end{align*} \end{split}\]

となるため、結局は最尤推定量 \(\hat{\mathbf{b}}_\mathrm{MLE}\) と同じものになります。実装上はunit devianceの平均を最小化する方が明快なため、例えばstatsmodelsにおける一般化線形モデルの最尤推定はこの方法で実装されています。また、scikit-learnなどではこの \(\hat{\mathbf{b}}_\mathrm{D}\) の計算式に適当な正則化項を付したもので \(\mathbf{b}\) の（正則化された）推定値を計算しています。

一般化線形モデルの評価

機械学習の文脈における一般化線形モデルの評価指標について、分析の目的次第では二乗誤差などの単純な指標を用いても良いのですが、そうでない場合は決定係数 \(R^2\) を拡張した 擬似 \(R^2\) (pseudo \(R^2\) ) と呼ばれる一連の指標が使われることがあります。擬似 \(R^2\) の定義には複数の流儀がありますが、いずれも一般化線形モデルの当てはまりの良さを ヌルモデル (null model) と呼ばれる自明なモデルのものと比較するものになっています。

一般化線形モデルに対するヌルモデルとは、たった1個のパラメータを用いて元のモデルと同じ確率分布 \(P\) を訓練データの目的変数の値 \(( y_i )_{i = 1}^N\) にうまく当てはまるようにしたモデルのことを指します。具体的には、訓練データの平均値 \(\bar{y} = \frac{1}{N} y_i\) を用いて

\[ y_i | x_i \sim P ( \mu = \bar{y} ) \]

となるようにした自明なモデルのことです。これは説明変数の値 \(( \mathbf{x}_i )_{i = 1}^N\) を用いずに線形予測子の「切片」に対応するパラメータ \(b_0\) のみを \(\hat{b}_0 = g ( \bar{y} )\) で当てはめたモデルと思うこともできます。

このヌルモデルによる対数尤度 \(\ell_0 (D)\) は

\[\begin{split} \begin{align*} \ell_0 ( D ) & = \log \left( \prod_{i = 1}^N p ( y_i ; \mu = \bar{y} ) \right) \\ & = \sum_{i = 1}^N \log p ( y_i ; \mu = \bar{y} ) \end{align*} \end{split}\]

と表せます。この \(\ell_0 ( D )\) は、訓練データ \(D\) のうち説明変数の値の情報を無視して単に確率分布 \(P ( \mu )\) を当てはめたときに達成する対数尤度の値と思うことができます。

擬似 \(R^2\) の計算に用いる当てはまりの良さの指標には複数の候補があります。尤度を用いるものは Cox-Snellの擬似 \(R^2\) (Cox-Snell pseudo \(R^2\) ) などと呼ばれ、

\[ R^2_\mathrm{CS} = 1 - \left( \frac{\exp ( \ell_0 ( \mathbf{b}; D ) )}{\exp ( \ell ( D ) )} \right)^{2 / N} \]

で定義されます。この指標はstatsmodelsなどで用いられているものです。

一方、逸脱度を用いるものは \(D^2\) や単に「擬似 \(R^2\) 」と呼ばれることが多く、

\[ D^2 = 1 - \frac{\mathrm{Dev} ( \mathbf{y}, \boldsymbol{\mu} ( \mathbf{b} ) )}{\mathrm{Dev} ( \mathbf{y}, \bar{\mathbf{y}} )} \]

で定義されます。分母の \(\mathrm{Dev} ( \mathbf{y}, \bar{\mathbf{y}} )\) はヌルモデルの逸脱度で、 \(\bar{\mathbf{y}} = ( \bar{y} )_{i = 1}^N\) とおきました。この指標はscikit-learnなどで用いられているものです。

なお、やはり機械学習の文脈での通例として、これらの評価指標を検証データや試験データに対して計算するときは、飽和モデルやヌルモデルのパラメータの決定に（訓練データではなく）検証データや試験データの目的変数の値を利用することに注意してください。

Pythonでの取り扱い

一般化線形モデルの推定については、

• statsmodelsなら GLM.fit()

• scikit-learnなら TweedieRegressor.fit()

など、どちらのライブラリでも他のモデルと同様の方法で行うことができます。

逸脱度 (deviance) の計算について、確率分布 \(P\) としてポアソン分布を用いた場合の実装をダミーのデータで確認してみましょう。

import matplotlib.pyplot as plt
import numpy as np

rng = np.random.default_rng(42)

n_samples = 20
y_true = rng.poisson(lam=10.0, size=(n_samples,))  # ダミーの目的変数の値
y_pred = rng.gamma(shape=2.0, scale=5.0, size=(n_samples,))  # ダミーの予測値

x = np.arange(n_samples)

fig, ax = plt.subplots()
ax.scatter(x, y_true, marker="o", c="C0", label="dummy obs.")
ax.scatter(x, y_pred, marker="x", c="C1", label="dummy pred.")
ax.set_title("Dummy Poisson Samples and Predicted Values")
ax.set_xlabel("Sample Index")
ax.set_ylabel("Value")
ax.set_xticks(x, labels=x)
ax.set_ylim(0, None)
ax.legend()

<matplotlib.legend.Legend at 0x3205f68a0>

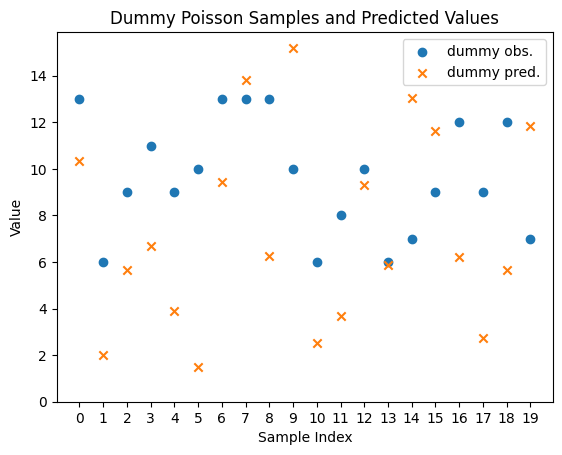
statsmodelsでは sm.families の各確率分布のクラス（ sm.families.Poisson など）に deviance() メソッドが実装されており、データ全体の逸脱度が計算されます。このメソッドの引数 endog には正しい目的変数の値 \(\mathbf{y}\) を、引数 mu には予測された条件つき期待値 \(\boldsymbol{\mu}\) をそれぞれ渡します。

# import statsmodels.api as sm

deviance_sm = sm.families.Poisson().deviance(endog=y_true, mu=y_pred)
print(deviance_sm)

76.27879279147069

scikit-learn ではTweedie分布の平均逸脱度を計算する関数

• metrics.mean_tweedie_deviance()

と、この関数のラッパーとして

• metrics.mean_poisson_deviance() 関数（ポアソン分布）と

• metrics.mean_gamma_deviance() 関数（ガンマ分布）

が実装されています。いずれも引数 y_true には正しい目的変数の値 \(\mathbf{y}\) を、引数 y_pred には予測された条件つき期待値 \(\boldsymbol{\mu}\) をそれぞれ渡します。

from sklearn.metrics import mean_poisson_deviance

mean_deviance_skl = mean_poisson_deviance(y_true=y_true, y_pred=y_pred)
print(n_samples * mean_deviance_skl)  # 比較のため、平均逸脱度をデータ全体の逸脱度に変換

76.27879279147069

擬似 \(R^2\) の計算について、statsmodelsでは GLM.fit() などの返り値である GLMResults クラスのオブジェクトにCox-Snellの擬似 \(R^2\) などの値を計算するメソッド GLMResults.pseudo_rsquared() が実装されています。一方、scikit-learnではTweedie分布に対して \(D^2\) を計算する関数 metrics.d2_tweedie_score() が実装されています。

小括

このページでは、一般化線形モデル (generalized linear model; GLM) と呼ばれるモデルの構成と、その推定と評価の方法についての概要を解説しました。また、その一環として逸脱度 (deviance) や擬似 \(R^2\) と呼ばれる指標とその計算方法を説明しました。分析対象のデータをよく観察する、ドメイン知識を利用するなどしてデータの生成過程に含まれそうな確率分布に目処がついている場合、一般化線形モデルのような統計的モデリングは有力な検討対象になります。実用上はポアソン回帰モデルやガンマ回帰モデルといった個別の具体的なモデルについての理解も重要なのですが、一般化線形モデルの全体像をつかんでおくことでモデル選択やモデル診断などの場面で役に立つことがあるかもしれません。

参考文献

• statsmodels - User Guide

  • Generalized Linear Models

• scikit-learn - User Guide

  • 1.1.12. Generalized Linear Models

  • 3.4.6.9. Mean Poisson, Gamma, and Tweedie deviances

  • 3.4.6.11. D2 score

• 久保拓弥 (2012). データ解析のための統計モデリング入門. 岩波書店.

  • 第3章 一般化線形モデル（GLM）