スパースモデリング（基本編）

オッカムの剃刀と過学習

かの有名な哲学者・神学者であるオッカム（英:William of Ockham 1285年-1347年）が多用した言葉に次の様なものがあります。

• ある事柄を説明するためには、必要以上に多くを仮定すべきではない。

• 必要がないなら多くのものを仮定してはならない。少数の論理でよい場合は多数の論理を定立してはならない。

不要な説明の存在を切り落とすことを比喩して「オッカムの剃刀」と言われたこの指針は、思考節約の原理、思考節約の法則、あるいは思考経済の法則、ときにはケチの原理とも呼ばれますが、本稿で取り扱うスパースモデリングの文脈では、まさに本質を突いた格言でもあると言えます。

「オッカムの剃刀」を体現した問題として、過学習の問題があります。
一般に、与えられた観測データに対して、学習モデルを複雑怪奇にすればするほど、学習モデルの表現力は増し、観測データをより良く表現するような学習モデルを作ることができます。
これは一見ものすごく良いことの様に聞こえますが、実際は必ずしも良いこととは言い切れません。
なぜならこの様な学習モデルは、今現在観測されているデータに対して当てはまりの良いモデルに過ぎず、いざ新しい未知のデータが与えられたとき（学習モデルを用いて予測を行うときなど）には全くトンチンカンな結果を返すモデルになり得るからです。

この様な問題を過学習と呼んだりします。
次の図は過学習が生じている例です（scikit-learn公式Examplesより）。

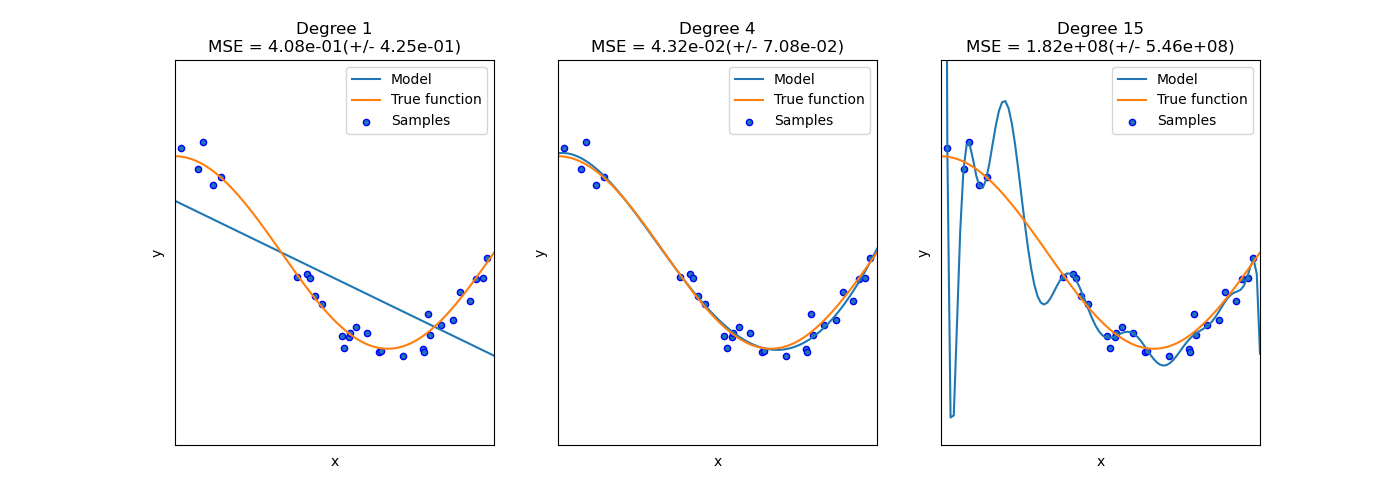
今観測データに対して、多項式回帰を行うことを考えており、図中のDegreeは多項式の次数を意味しています。
右のモデルはシンプルな一方、サンプルデータに対してフィットはしていません。
degree=1（単回帰）、すなわち1次関数では直線しか引けないので、さすがに表現力としては力不足を感じます。
左のモデルは表現力が高く、サンプルデータに対してとてもフィットしているように見えます。
しかし、未知のデータに対しての予測には適応できず、実際未知データに対する誤差（ここではMSE）は発散しています。
中央のモデルは両者と比較すると最もサンプルデータにフィットしているように見えます。
すなわち、表現力が高過ぎても（もちろん低過ぎても）あんまり筋の良い学習とは言えないということが読み取れます。
汎化性能（未知のデータへの予測）が高いモデルを作成するには、「オッカムの剃刀」的なSimple is BESTな発想を機械学習のモデルに取り込む必要があります。

スパースモデリングとは？

スパースモデリングとは過学習を回避できる手法のひとつです。
スパースモデリングを用いることで、多くの要因の中の本質的な少数の要因の組み合わせを見つけ出したり、基本となる要因を発見することができます。
もう少し熟れた表現をすると、高次元データに内在する本質的な低次元性を利用し、目的の学習に必要な情報を持っている低次元部分空間をあぶり出すことで、不必要な情報やノイズを除去したシンプルな学習モデルを構築します。
このように、仮定している学習モデル内のパラメータから本質的でないものを削ぎ落とし（不要なパラメータは0と推定し）、最終的な推定解に0がたくさん含まれることを想定しているので、スパース（=疎な）モデリングと呼ばれます。
実際のスパースモデリングでは、通常の誤差関数\(E(\omega)\)に正則化項\(\Omega(\omega)\)と呼ばれるスパースな解を誘導するペナルティを加えた、次の目的関数\(L(\omega)\)の最小化を考えます。

\[ L(\omega)=E(\omega)+\alpha\Omega(\omega) \]

ここで、\(\alpha\)は一般に正則化係数と呼ばれ、正則化項の影響力の強さ、スパースな解への誘導力の強さを調整するハイパーパラメータ（正値）です。

例えば、最も一般的なスパースモデリングであるLASSO（誤差関数が残差二乗和の場合）では、具体的な関数形は次の様になります。
サンプル数を\(N\)、パラメータ数を\(P\)とし、サンプル数\(N\)の影響を排除するために誤差関数\(E(\omega)\)は\(N\)で除してスケーリングされているとします。

\[\begin{split} \begin{align} E(\omega)&=\frac{1}{2N}\|y-X\omega\|_2^2\\ \Omega(\omega)&=\|\omega\|_1=\sum_p^P|\omega_p| \end{align} \end{split}\]

結局、解くべき最適化問題は以下の様に記述されます。

\[ \min_{\omega}\frac{1}{2N}\|y-X\omega\|_2^2+\alpha\|\omega\|_1 \]

最適化問題の視覚的意味

スパースモデリングで登場する最適化問題を視覚的に理解するには、ラグランジュの未定乗数法という手法が便利です。
ラグランジュの未定乗数法についての詳細は別の良書に譲りますが、ラグランジュの未定乗数法の考え方を用いることで、先ほどの最適化問題は次の不等式制約付き最適化問題と等価であることがわかります。

\[ \min_{\omega}E(\omega)+\alpha\Omega(\omega)\:\:\Leftrightarrow\:\:\min_{\omega}E(\omega)\:\:\:\mathrm{s.t.}\:\Omega(\omega)\leq\rho \]

すなわち、\(\Omega(\omega)\leq\rho\)の制約領域内で\(E(\omega)\)を最小化する問題と等価になります（\(\rho\)はハイパーパラメータ\(\alpha\)に依存して決まる）。

先ほど例示したLASSOでは、視覚的には以下の問題を考えていることと同値になります。

\[ \min_{\omega}\frac{1}{2N}\|y-X\omega\|_2^2\:\:\:\mathrm{s.t.}\:\|\omega\|_1\leq\rho \]

このことを図を用いて解釈してみます。

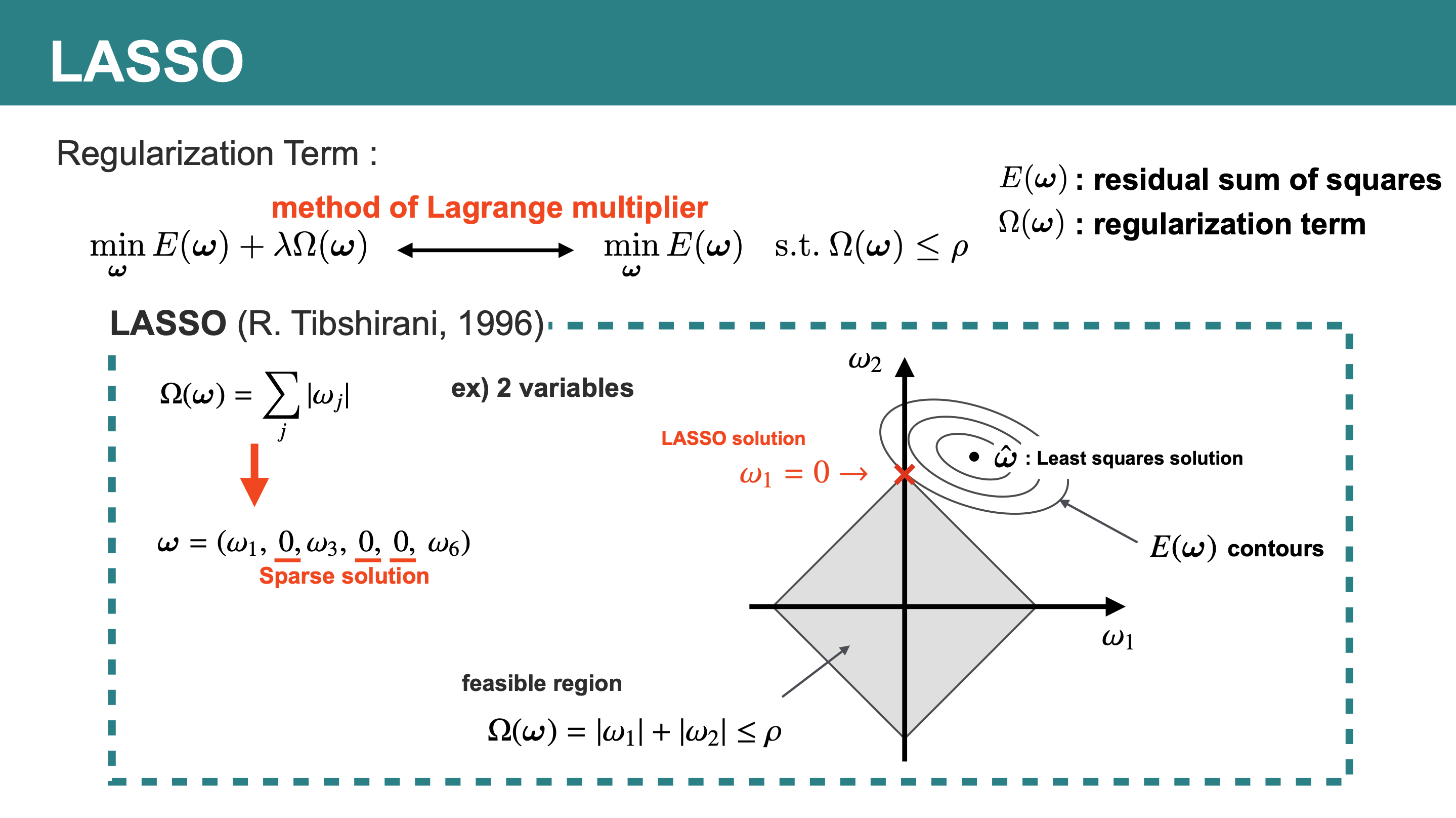
まず制約領域\(\Omega(\omega)\leq\rho\)ですが、これは図中の灰色の図形(feasible region)に対応します。
LASSOでは\(\Omega(\omega)=|\omega_1|+|\omega_2|\leq\rho\)の領域となるので、図の様な軸上に角がある正方形となります。
次に\(E(\omega)\)ですが、こちらは\(E(\omega)\)の等高線（contours）を描くと、最小二乗解\(\hat{\omega}=\mathrm{arg}\min_{\omega}E(\omega)\)（Least squares solution）を中心として同心円状の形となります。
元の問題に立ち返ると、\(\Omega(\omega)\leq\rho\)の制約領域内で\(\min_{\omega}E(\omega)\)を解くのが目標でしたので、図の×印が求める解（LASSO solution）となります。
この場合、得られるLASSO解は\(\omega_1=0\)のスパースな解となることが視覚的にも明らかです。

ではなぜ、この例でスパースな解が得られたのでしょうか。
直感としては制約領域\(\Omega(\omega)\leq\rho\)に角があり、その角で誤差関数\(E(\omega)\)が最小となりやすいからだと読み解くことができます。
熟れた言い方をすると、正則化項\(\Omega(\omega)\)に微分不可能な点が存在することが、スパース性を誘導するためには重要であると言うことができます。
スパースモデリングでは、この制約領域\(\Omega(\omega)\leq\rho\)の構造を変化させてさまざまなアレンジを行うことができます。

データの読み込み

import warnings

warnings.filterwarnings("ignore")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# matplotlibでは日本語にデフォルトで対応していないので、日本語対応フォントを読み込む
plt.rcParams["font.family"] = "BIZ UDGothic"  # Windows
# plt.rcParams['font.family'] = 'Hiragino Maru Gothic Pro' # Mac

# その他使えるフォント一覧は以下のコードで取得できます。
# import matplotlib.font_manager
# [f.name for f in matplotlib.font_manager.fontManager.ttflist]

pd.set_option("display.max_rows", 10)
pd.set_option("display.max_columns", 10)

fpath = "../data/2020413.csv"
df = pd.read_csv(fpath, index_col=0, parse_dates=True, encoding="shift-jis")[::5]

データ数が多いので、今回は1秒単位のデータを1/5に間引き、5秒単位のデータとして利用することとします。
まずは使用するデータの要約統計量を確認します。

df.describe()

	気化器圧力_PV	気化器圧力_SV	気化器圧力_MV	気化器液面レベル_PV	気化器液面レベル_SV	...	反応器流入組成（HAc）_PV	セパレータ蒸気排出量_MV (Fixed)	アブソーバスクラブ流量_MV (Fixed)	アブソーバ還流流量_MV (Fixed)	気化器液体流入量_MV (Fixed)
count	17281.000000	17281.000000	17281.000000	17281.000000	1.728100e+04	...	17281.000000	17281.0000	17281.000000	17281.000000	1.728100e+04
mean	128.007284	128.003389	18.739799	0.699812	7.000000e-01	...	0.109528	16.1026	15.119858	0.755958	2.192400e+00
std	0.730465	0.527738	0.271421	0.001450	1.110255e-16	...	0.000585	0.0000	0.013176	0.015597	4.441021e-16
min	125.086386	126.183125	17.648103	0.692279	7.000000e-01	...	0.107120	16.1026	14.119800	0.726000	2.192400e+00
25%	127.522881	127.638520	18.558082	0.699343	7.000000e-01	...	0.109153	16.1026	15.119800	0.746000	2.192400e+00
50%	128.021441	128.030307	18.739989	0.699980	7.000000e-01	...	0.109519	16.1026	15.119800	0.756000	2.192400e+00
75%	128.519622	128.403574	18.921879	0.700581	7.000000e-01	...	0.109892	16.1026	15.119800	0.766000	2.192400e+00
max	130.404329	129.356617	19.774625	0.704532	7.000000e-01	...	0.112416	16.1026	16.119800	0.786000	2.192400e+00

8 rows × 91 columns

このままだとカラム数も多く多重共線性の恐れも高いため、次元削減に沿ってカラムを減らしてみます。詳細は次元削減を適宜参照してください。

# std < 1e-10の数値列をdropする
drop_list = list(df.describe().loc["std"] < 1e-10)
df = df.drop(columns=df.columns[drop_list])

# 相関行列の要素のうち、条件を満たすものを要素を1、満たしていない要素を0とする、隣接行列を取得する。
# ここでは、後の計算の簡略化のために対角成分も残したまま取り扱う。
# 今回は相関係数の絶対値が0.85より大きいことを条件とする。
Adjacency = np.array(df.corr().abs() > 0.85).astype("int")

# グラフ理論によると隣接行列のべき乗（ただし非ゼロ要素は都度すべて1に変換する）は、適当回数遷移した後に接続している要素を示す。
# 例えばi行の非ゼロ要素のインデックス集合は、i番目の要素と接続している要素の集合となる。
# これを利用して、先ほど定義した隣接行列から、多重共線性の危険性のある列のグループを抽出する
while True:
    Adjacency_next = np.dot(Adjacency, Adjacency).astype("int")
    Adjacency_next[Adjacency_next != 0] = 1
    if np.all(Adjacency_next == Adjacency):
        break
    else:
        Adjacency = Adjacency_next

multicol_list = [np.where(Ai)[0].tolist() for Ai in Adjacency]

# 要素が1つだけのグループ、および重複のあるグループを取り除き、インデックスの最も若い列を残して、それ以外を削減対象とする。
# 削減対象以外の残す列のインデックスを取得する。
extract_list = sorted(list(set(sum([m[:1] for m in multicol_list], []))))

# 多重共線性の危険性を排除したデータセットを得る。
df_corr = df.iloc[:, extract_list]

# 以降では相関係数で次元削減したデータセットを用いる
df = df_corr.copy()

ここでは 気化器圧力_PV を予測対象である目的変数とし、 気化器圧力_PV を除いた他のすべての列を説明変数とします。
すなわち、基本的な回帰モデルで言うところの、分布ラグモデルを今回は考えることとします。詳細は基本的な回帰モデルを適宜参照してください。
説明変数と目的変数の分割、さらには訓練データと検証データへの分割を行います。
なお今回は訓練データ前半80％、検証データ後半20%として分割し、説明変数を X ＆目的変数を y としています。

from sklearn.model_selection import train_test_split

X_train, X_validation, y_train, y_validation = train_test_split(
    df[df.columns.difference(["気化器圧力_PV"])],
    df[["気化器圧力_PV"]],
    test_size=0.2,
    shuffle=False,
)

またデータのスケールを合わせるために正規化を行います。詳細は正規化を適宜参照してください。

from sklearn.preprocessing import StandardScaler

# 正規化を行うオブジェクトを生成
SS_X_train = StandardScaler()
SS_X_validation = StandardScaler()
SS_y_train = StandardScaler()
SS_y_validation = StandardScaler()

# fit_transform関数は、fit関数（正規化するための前準備の計算）と
# transform関数（準備された情報から正規化の変換処理を行う）の両方を行う
X_train[:] = SS_X_train.fit_transform(X_train)
X_validation[:] = SS_X_validation.fit_transform(X_validation)
y_train[:] = SS_y_train.fit_transform(y_train)
y_validation[:] = SS_y_validation.fit_transform(y_validation)

さらに時系列データの時間遅れを考慮して学習モデルを構築するために、前処理として時間窓切り出し処理を行います。処理の詳細は時間窓切り出し処理の記事に記載しており、そこで定義したものと同じ time_window_transform() 関数を用いて変換を行うこととします。

変換に使う各パラメータについては次のように指定します。

「元のデータを平滑化せずそのまま使用 ( L=1 ) し、12ステップ ( M=12 ) すなわち60秒遅れ(=12ステップ×5秒/1ステップ)までの説明変数を用いて、1ステップ ( N=1 ) 5秒先の未来の目的変数mの値を予測するような学習モデルを考える。この際、データのスキップは行わない ( S=1 ) 。」

Show code cell source Hide code cell source

# import numpy as np


# L が M の約数になっていなかった場合は例外処理に回す
class LMUndivisibleError(Exception):
    pass


def time_window_x(x, l, m, n, s):

    nrow, ncol = x.shape
    nsample_org = nrow - m + 1 - n  # 元データの切り出しに使われる範囲のサイズ
    nsample = (nrow - m - n) // s + 1  # 出力のサンプル数

    # l が m の約数になっていなかった場合は例外を発生
    nsplit, rem = divmod(m, l)
    if rem != 0:
        raise LMUndivisibleError

    # 説明変数
    x_transformed = np.zeros((nsample, nsplit, ncol), dtype=float)  # 出力の格納先
    for i, st in enumerate(range(0, nsample_org, s)):
        en = st + m
        tmpX = x[st:en, :]
        # L ごとに切って配列の次元を増やしたあと平均して次元をもとに戻す
        x_transformed[i, :, :] = tmpX.reshape(nsplit, l, ncol).mean(axis=1)

    return x_transformed


def time_window_y(y, m, n, s):

    res = y[n + m - 1 :: s, :].reshape((-1, 1))
    return res


def time_window_transform(x, y, l, m, n, s):

    if m % l != 0:
        raise LMUndivisibleError

    x_transformed = time_window_x(x, l, m, n, s)
    nrow = x_transformed.shape[0]
    y_transformed = time_window_y(y, m, n, s)[:nrow, :]

    return x_transformed, y_transformed

L, M, N, S = 1, 12, 1, 1

X_train_lmns, y_train_lmns = time_window_transform(
    X_train.values, y_train.values, l=L, m=M, n=N, s=S
)
X_validation_lmns, y_validation_lmns = time_window_transform(
    X_validation.values, y_validation.values, l=L, m=M, n=N, s=S
)

time_window_transform() では説明変数Xが３次元テンソルとなって返ってくるので、以後の学習モデルに適用できるように２次元にフラット化します。
ここでは窓方向にフラット化することとします。こちらも詳細は時間窓切り出し処理を適宜参照してください。

X_train_lmns_flat = X_train_lmns.reshape(
    len(X_train_lmns), int(X_train_lmns.size / len(X_train_lmns)), order="F"
)
X_validation_lmns_flat = X_validation_lmns.reshape(
    len(X_validation_lmns),
    int(X_validation_lmns.size / len(X_validation_lmns)),
    order="F",
)

本項では、ハイパーパラメータ（後述）がいくつか出てきます。
これらのチューニング＆モデル評価については、本項では割愛し別の記事回帰モデルの評価やクロスバリデーション（交差検証）などに譲ることとします。

よく使用する関数

今回は学習モデルの性能を確認する関数として score 関数を事前に用意しました。
score 関数に検証データの目的変数（実測値）と、説明変数と学習モデルから出力される目的変数の予測値を入力することで、下記のモデル評価スコアを計算します。各スコアの詳細は回帰モデルの評価にまとめられています。

• MAE：平均絶対誤差

• RMSE：二乗平均平方根誤差

• CORR：相関係数

• R2：決定係数

さらに実測値と予測値をグラフで可視化します。

from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

x_tick_label = pd.date_range(
    y_validation.index[0], y_validation.index[-1], freq="10min"
)
x_tick_loc = [y_validation.index.get_loc(label) for label in x_tick_label]


def score(y, y_hat):
    mae = mean_absolute_error(y, y_hat)
    rmse = np.sqrt(mean_squared_error(y, y_hat))
    corr = np.corrcoef(y, y_hat, rowvar=False)[0, 1]
    r2 = r2_score(y, y_hat)

    print(f"MAE\t: {mae}")
    print(f"RMSE\t: {rmse}")
    print(f"CORR\t: {corr}")
    print(f"R2\t: {r2}")

    plt.figure(figsize=[8, 6], dpi=200)
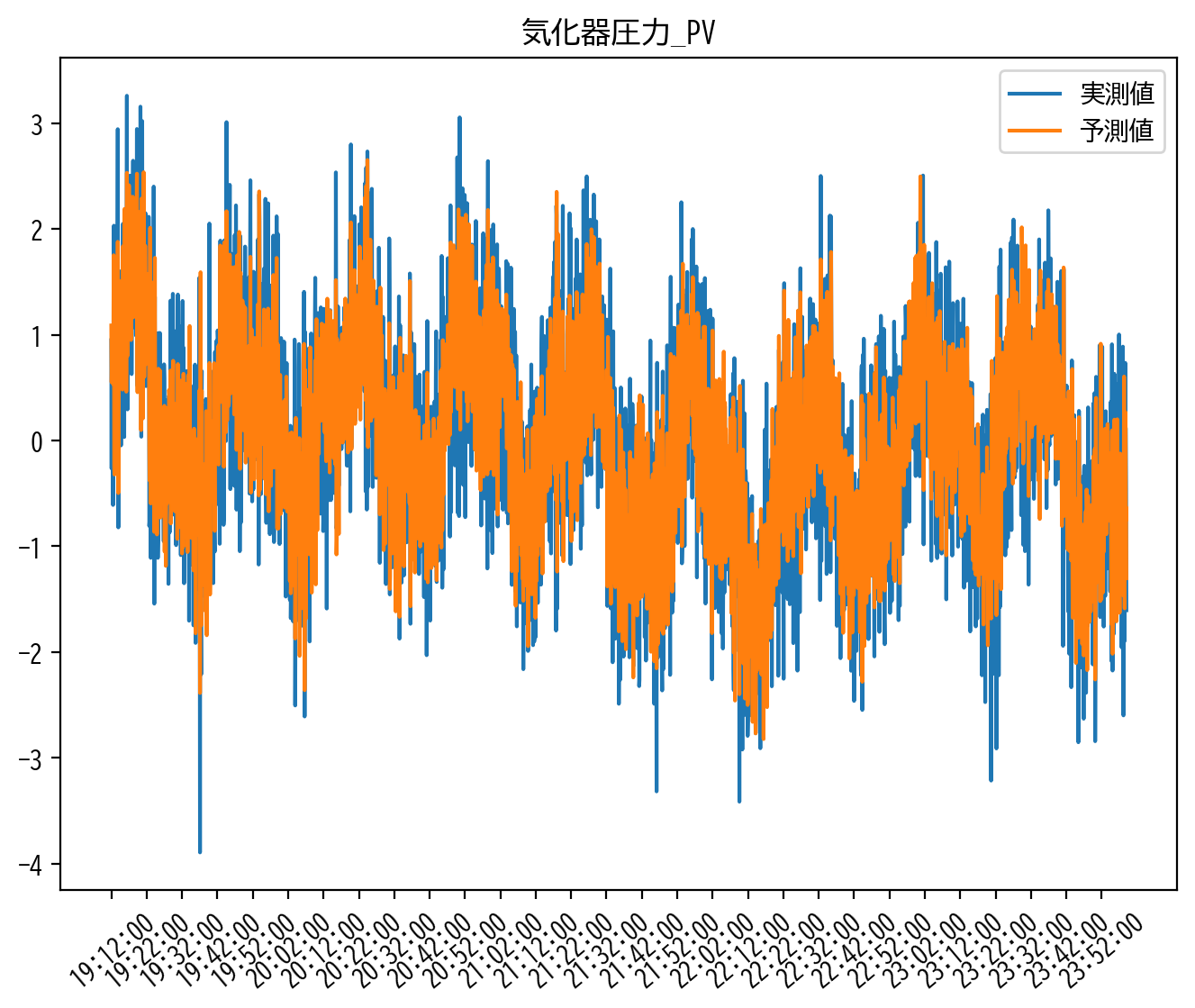
    plt.plot(y, label="実測値")
    plt.plot(y_hat, label="予測値")
    plt.title("気化器圧力_PV")
    plt.xticks(x_tick_loc, x_tick_label.strftime("%H:%M:%S"), rotation=40)
    plt.legend()
    plt.show()

    return pd.DataFrame(
        np.array([[mae, rmse, corr, r2]]), columns=["mae", "rmse", "corr", "r2"]
    )

さらに学習モデルのパラメータを可視化する関数として heatmap 関数を用意しました。
こちらは、学習モデルのパラメータを入力することで、時間遅れを明示的に示したヒートマップを図示します。
赤色は正値、青色は負値、色の濃さは値の大きさを意味し、白色は0です。
scale オプションを指定すると、ヒートマップの色は [-scale, scale] の範囲に限定されます。

def heatmap(coef, scale=None):
    plt.figure(figsize=[8, 6], dpi=200)
    if scale is None:
        sns.heatmap(coef.reshape(X_validation.shape[1], -1), center=0, cmap="bwr")
        plt.title("各パラメータ $\omega_i$ の推定値")
    else:
        sns.heatmap(
            coef.reshape(X_validation.shape[1], -1),
            center=0,
            cmap="bwr",
            vmin=-scale,
            vmax=scale,
        )
        plt.title(f"各パラメータ $\omega_i$ の推定値：色調範囲[{-scale}, {scale}]")
    plt.xticks(
        np.arange(M) + 0.5,
        [f"-{(m+1)*5}s ~ -{m*5}s" for m in np.arange(M)][::-1],
        rotation=10,
        fontsize=5,
    )
    plt.yticks(
        np.arange(X_validation.shape[1]) + 0.5,
        X_validation.columns,
        rotation=0,
        fontsize=5,
    )
    plt.xlabel("窓内の時間遅れ")
    plt.ylim(X_validation.shape[1], 0)
    plt.grid()
    plt.show()

また正則化係数とパラメータの推定解の関係を可視化するために path 関数を用意しました。
横軸を正則化係数 alpha とし、縦軸を個々のパラメータの推定解としています。（ただし、横軸は対数スケールであることに注意。）
すべてのパラメータを可視化すると図が解読困難となることが予想されるため、ここでは各列毎に窓内で最も時間的に新しいもの、すなわち本稿では -5s ~ -0s のみを図示することとします。

def path(alphas, coefs, best=None):
    coefs = coefs[0, M - 1 :: M]
    plt.figure(figsize=[8, 6], dpi=200)
    plt.xscale("log")
    plt.xlim(np.min(alphas), np.max(alphas))
    plt.ylim(np.min(coefs), np.max(coefs))
    for coef in coefs:
        plt.plot(alphas, coef)
    if not best is None:
        plt.vlines(
            best,
            np.min(coefs),
            np.max(coefs),
            linestyles="dashed",
            label="最適な正則化係数",
        )
    plt.xlabel("正則化係数 " + "$\\alpha$" + "  [log scale]")
    plt.ylabel("各パラメータ $\omega_i$ の推定値")
    plt.title("正則化係数に応じた推定解のパス（軌跡）")
    plt.legend()
    plt.grid()
    plt.show()

最後にラグランジュの未定乗数法に基づいた、制約領域と最適解（および最小二乗解）の関係性を図示する関数も用意しました。
f(x,y)=0 の解が制約領域の境界となる関数（ x-y 平面内）をsympyで定義してfに入力すると、num (= 10)個の学習モデルに対する最適解（および最小二乗解と等高線）を示します。
例えば\(\Omega(\omega)=|\omega_1|+|\omega_2|\leq1\)は\(f(x,y)=|x|+|y|-1\)として、 f = sympy.Abs(x) + sympy.Abs(y) - 1 を入力とします。
なお、個々の点の色の違いは個々の学習モデルを明示的に分けて表現するためで、それ以外の意味はありません。
ただし、最適解が最小二乗解と一致する場合のみ黒色にしました。

import sympy
from scipy.optimize import fsolve
from scipy.optimize import minimize


def image(f=None, num=10, seed=3, scale=3):

    def const(f):
        delta = 0.001
        x, y = sympy.symbols("x y", real=True)
        f_y = sympy.solve(f, x)
        for fy in f_y:
            domain = sympy.solve(fy, y)
            if len(domain) > 1:
                break
        constraint = (
            np.array(
                [
                    [[p, fy.subs(y, p)] for fy in f_y]
                    for p in np.arange(domain[0], domain[1], delta)
                ]
            )
            .reshape(-1, 2)
            .astype(np.float32)
        )
        return constraint[~np.isnan(constraint).any(axis=1), :], domain

    def plot_implicit(f, fill=False):
        delta = 0.01
        P1, P2 = np.meshgrid(
            np.arange(-scale, scale, delta), np.arange(-scale, scale, delta)
        )
        if fill:
            plt.contourf(
                P1,
                P2,
                sympy.lambdify(sympy.symbols("x y", real=True), f, "numpy")(P1, P2),
                [-np.inf, 0],
                colors=["lightgray"],
            )
        else:
            plt.contour(
                P1,
                P2,
                sympy.lambdify(sympy.symbols("x y", real=True), f, "numpy")(P1, P2),
                [0],
                colors=["black"],
                linewidths=1,
            )

    np.random.seed(seed=seed)
    y = np.random.normal(size=[num, 2]) * 3
    X = np.random.normal(size=[num, 2, 2])
    Eopt = np.vstack([np.linalg.inv(X[n].T @ X[n]) @ X[n].T @ y[n] for n in range(num)])

    use_index = np.all(np.abs(Eopt) < scale, axis=1)
    y, X, Eopt, num = y[use_index], X[use_index], Eopt[use_index], np.sum(use_index)

    constraint, domain = const(f)

    plt.figure(figsize=[8, 6], dpi=200)
    plt.gca().set_aspect("equal")
    Ecross = np.zeros(Eopt.shape)
    if not f is None:
        for n in range(num):
            best = np.argmin(
                np.linalg.norm(
                    np.tile(y[n].reshape(2, -1), len(constraint)) - X[n] @ constraint.T,
                    axis=0,
                )
                ** 2
            )
            if (
                sympy.lambdify(sympy.symbols("x y", real=True), f, "numpy")(
                    Eopt[n, 0], Eopt[n, 1]
                )
                > 0
            ):
                Ecross[n] = constraint[best]
                p1, p2 = sympy.symbols("x y", real=True)
                E = sympy.Matrix(y[n]) - sympy.Matrix(X[n]) * sympy.Matrix(
                    np.array([[p1], [p2]])
                )
                E = (E.T * E)[0] - np.linalg.norm(y[n] - X[n] @ Ecross[n]) ** 2
                plot_implicit(E)
            else:
                Ecross[n] = Eopt[n]

            plot_implicit(f, fill=True)

    inner_index = np.where(Ecross[:, 0] == Eopt[:, 0])[0]

    RMSE_rate = np.mean(np.all(Ecross == Eopt, axis=1))
    sparse_rate = np.mean(np.any(np.abs(np.abs(Ecross) - domain) < 1e-3, axis=1))
    non_sparse_rate = 1 - RMSE_rate - sparse_rate

    plt.xlim(-scale, scale)
    plt.ylim(-scale, scale)
    plt.xlabel("$\omega_1$")
    plt.ylabel("$\omega_2$")
    plt.grid()
    plt.scatter(Eopt[:, 0], Eopt[:, 1], c=np.arange(len(Eopt)), cmap="hsv", alpha=0.2)
    plt.scatter(Ecross[:, 0], Ecross[:, 1], c=np.arange(len(Eopt)), cmap="hsv")
    plt.scatter(Ecross[inner_index, 0], Ecross[inner_index, 1], c="black")
    # plt.text(-2.8, 2.3, '　制約領域の大きさ:'+format(round(float(domain[1]),3), '0<5')
    #         +'\n　最小二乗解の割合:'+format(round(RMSE_rate,3), '0<5')
    #         +'\n　スパース解の割合:'+format(round(sparse_rate,3), '0<5')
    #         +'\n非スパース解の割合:'+format(round(non_sparse_rate,3), '0<5'), fontsize=7)
    plt.show()

Least Squares Method

まずは、ベースライン＆復習も兼ねて、通常の最小二乗法を用いて回帰を行います。
最小化すべき目的関数は以下のように与えられます。

\[ \min_{\omega}\frac{1}{2N}\|y-X\omega\|_2^2 \]

さらに推定解は解析的に求めることができます。

\[ \hat{\omega}=(X^{\top}X)^{-1}X^{\top}y \]

Pythonでは最小二乗法をお手軽に行うために sklearn.linear_model に LinearRegression クラスが用意されています。

from sklearn.linear_model import LinearRegression

LinearRegression_model = LinearRegression()
LinearRegression_model.fit(X_train_lmns_flat, y_train_lmns)
score_LR = score(
    y_validation_lmns, X_validation_lmns_flat @ LinearRegression_model.coef_.T
)

MAE	: 0.4538426816576046
RMSE	: 0.5735827479880623
CORR	: 0.8256992593249889
R2	: 0.6713850541086416

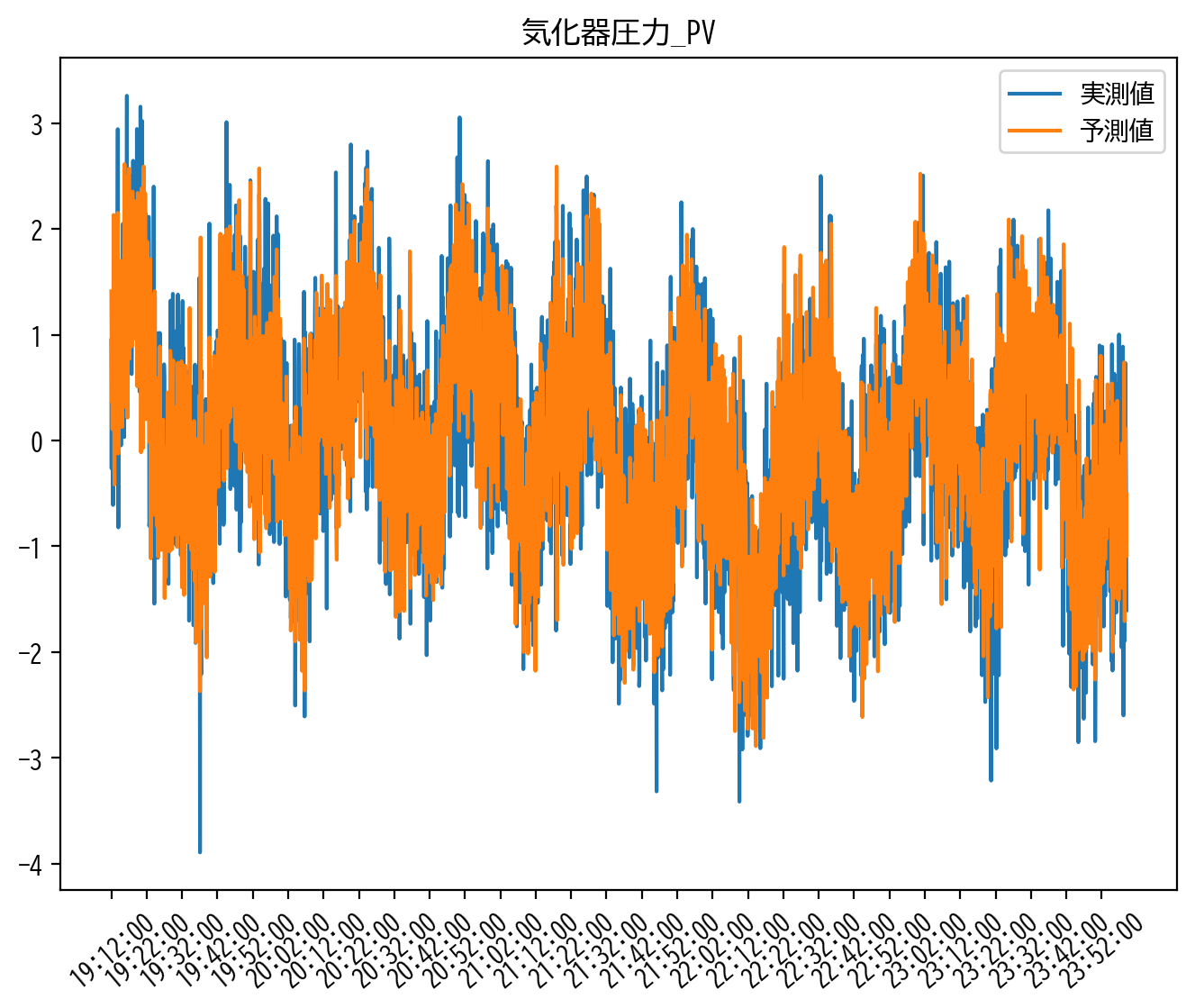
heatmap(LinearRegression_model.coef_)

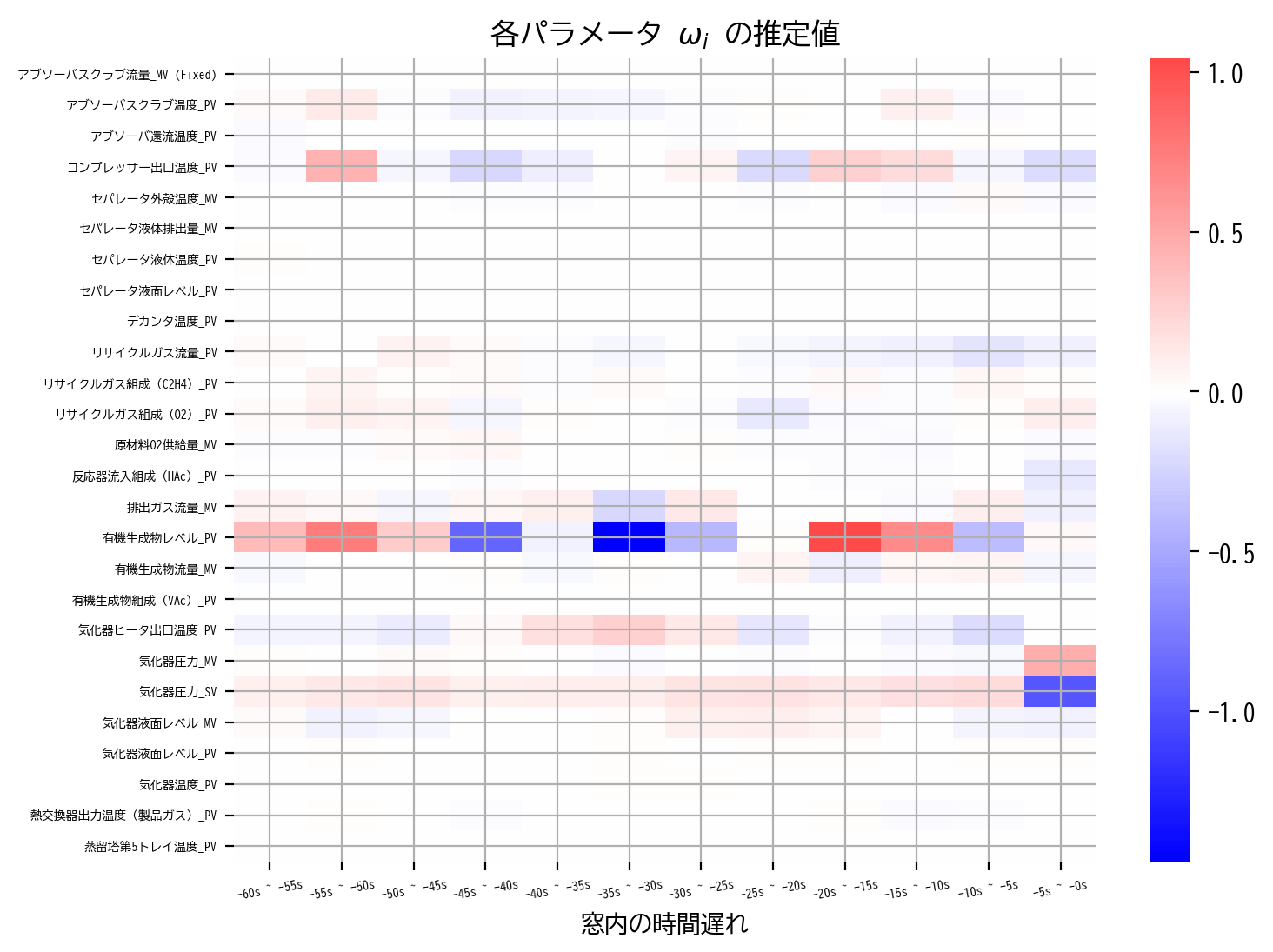
heatmap(LinearRegression_model.coef_, scale=0.5)

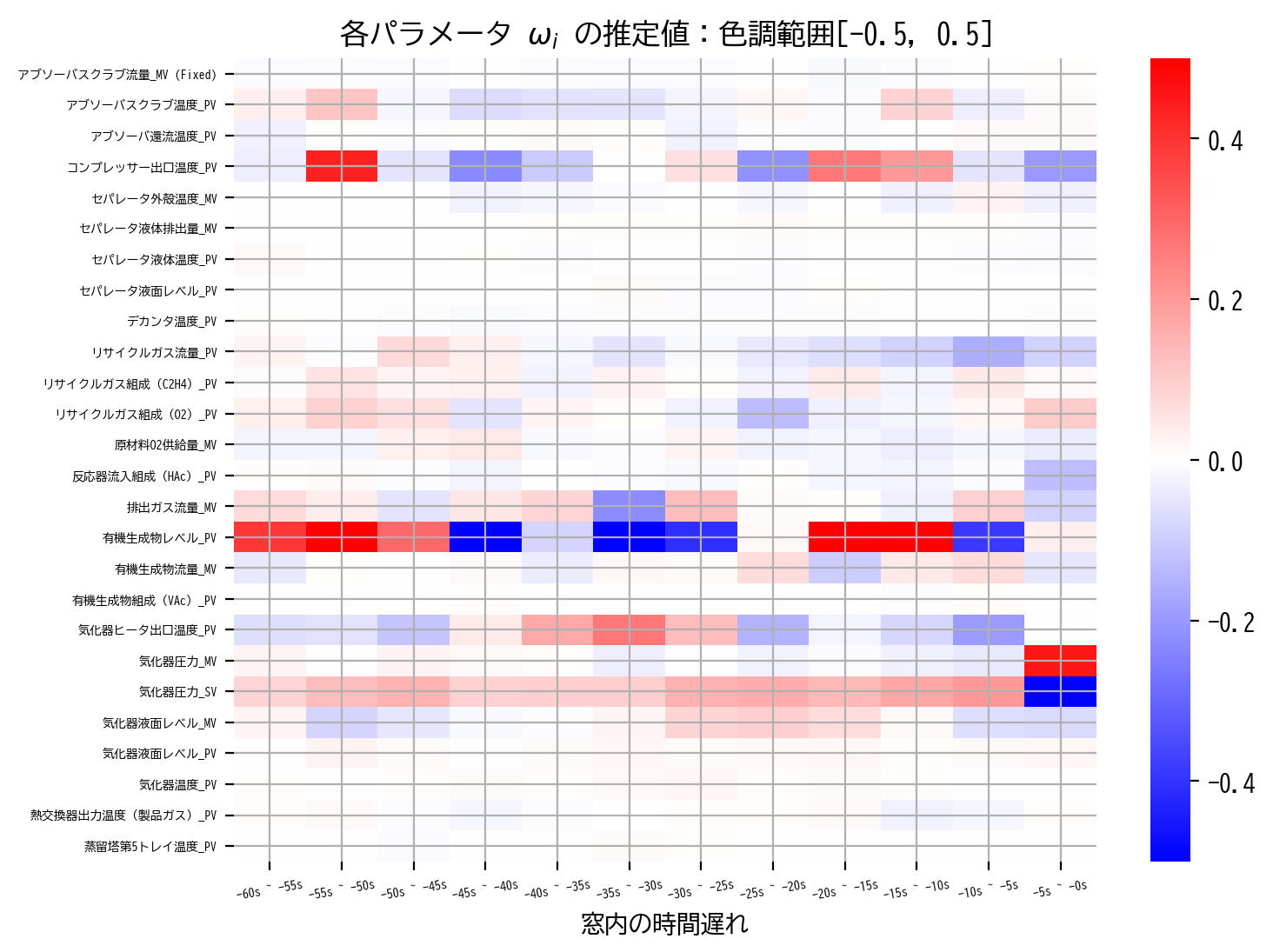
次元削減でも取り上げましたが、説明変数間に強い相関がある場合には多重共線性の影響を心配する必要があります。
特に今回の様に時系列データ解析で窓を用いる場合などは、窓内の時間方向（ヒートマップ内の横軸方向）に大変強い相関（自己相関）が生じるため、通常の最小二乗法の結果だけでは信憑性に欠けます。
信憑性に欠ける理由はさまざまがありますが、例えばヒートマップ内の 有機生成物レベル_PV の結果を見てみると直感的に分かりやすいかもしれません。
有機生成物レベル_PV の推定値を窓方向に見てみると、赤と青を繰り返す、すなわち正の値と負の値を交互に繰り返していることが読み取れます。
これは時間的に隣り合う変数同士の相関が非常に強いため、実際には目的変数に極端に影響を与えていないにも関わらず、そのことを学習モデルでは前後の正負の打ち消し合いで表現しているのではと読み取ることができます。
これでは 有機生成物レベル_PV 全体として目的変数に与える影響は捉えられているかもしれませんが、窓内の個々の時間遅れが実際にどの程度目的変数に影響を与えたかについては疑わしい結果といえるでしょう。
さらに、scale=0.5 で色調範囲を拡大すれば、同様の現象が他の列でも生じていることが読み取れます。

RIDGE

スパースモデリングに入る前に、スパースな解を誘導しないものの、過学習を抑えることのできる手法としてRIDGE回帰を紹介します。
制約領域などの基本的な考え方は、本稿冒頭で紹介したLASSO回帰と同じですが、RIDGE回帰では以下の様な個々のパラメータの二乗和を正則化項とします。

\[ \min_{\omega}\frac{1}{2N}\|y-X\omega\|_2^2+\frac{\alpha}{2}\|\omega\|_2^2 \]

すなわち、ある半径をもつ原点を中心とした円が制約領域となります。
そのため、境界はいたるところ滑らかなので、LASSOのようなスパースな推定解にはならないものの、制約領域の影響でパラメータの過大評価を抑えられ、過学習が起きにくい安定な学習を行うことができます。
実はRIDGE回帰も推定解を解析的に求めることができ、以下の様に与えられます。

\[ \hat{\omega}=(X^{\top}X+\alpha I)^{-1}X^{\top}y \]

そのため、計算コストが非常に小さくすむのも特徴です。
では、実際に最適化問題を図示してみます。
この図では薄い点が最小二乗解を、濃い点が対応するRIDGE回帰解を示していることに注意してください。

x, y = sympy.symbols("x y", real=True)
Omega_L2 = x**2 + y**2 - 1**2
image(Omega_L2)

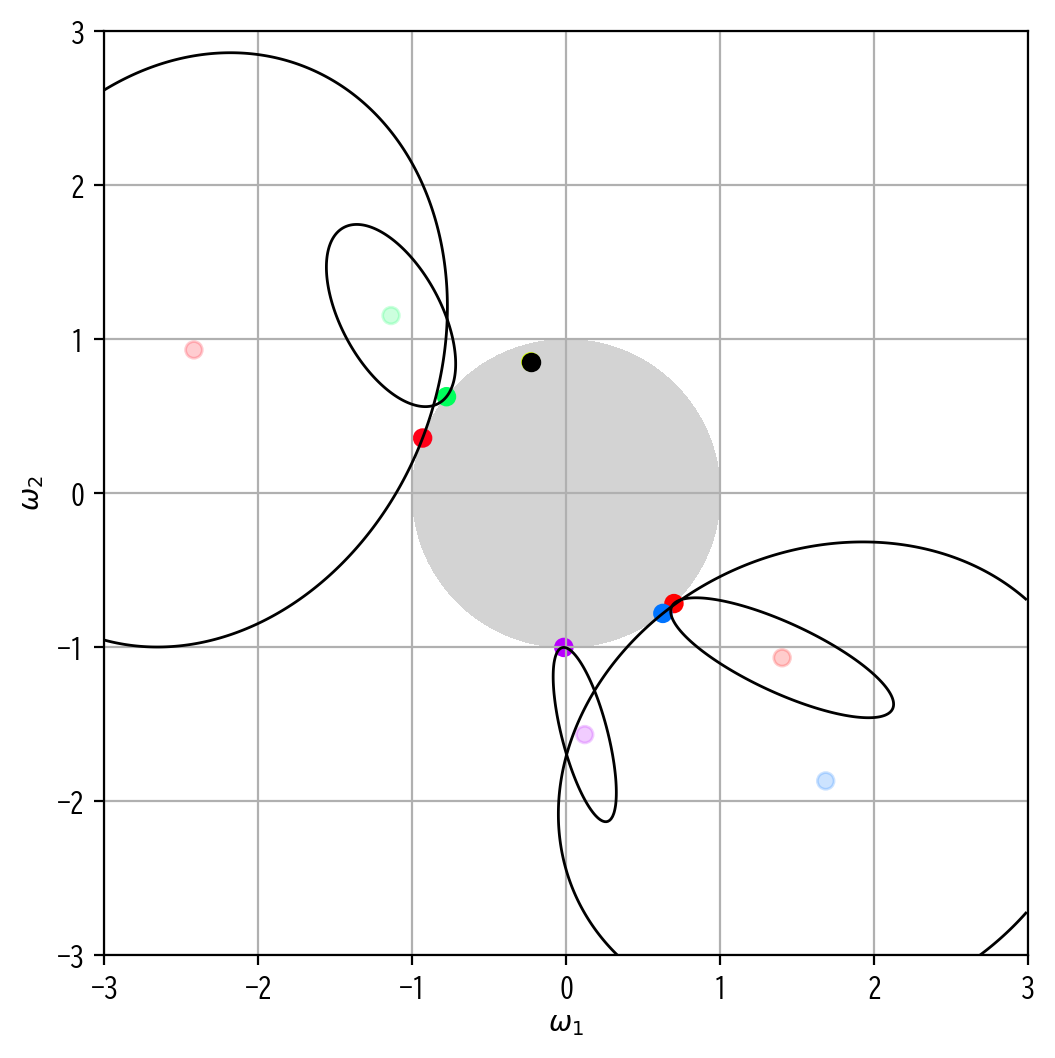
円状の制約領域内で誤差関数\(E(\omega)\)の最小化を試みた結果、全体的にパラメータは縮小推定されていることが明らかです。
学習モデルを100個用意して、この制約領域を縮めていったとき、すなわち\(\alpha\to\infty\)とした場合の、パラメータの推定解の挙動は以下の様になります。

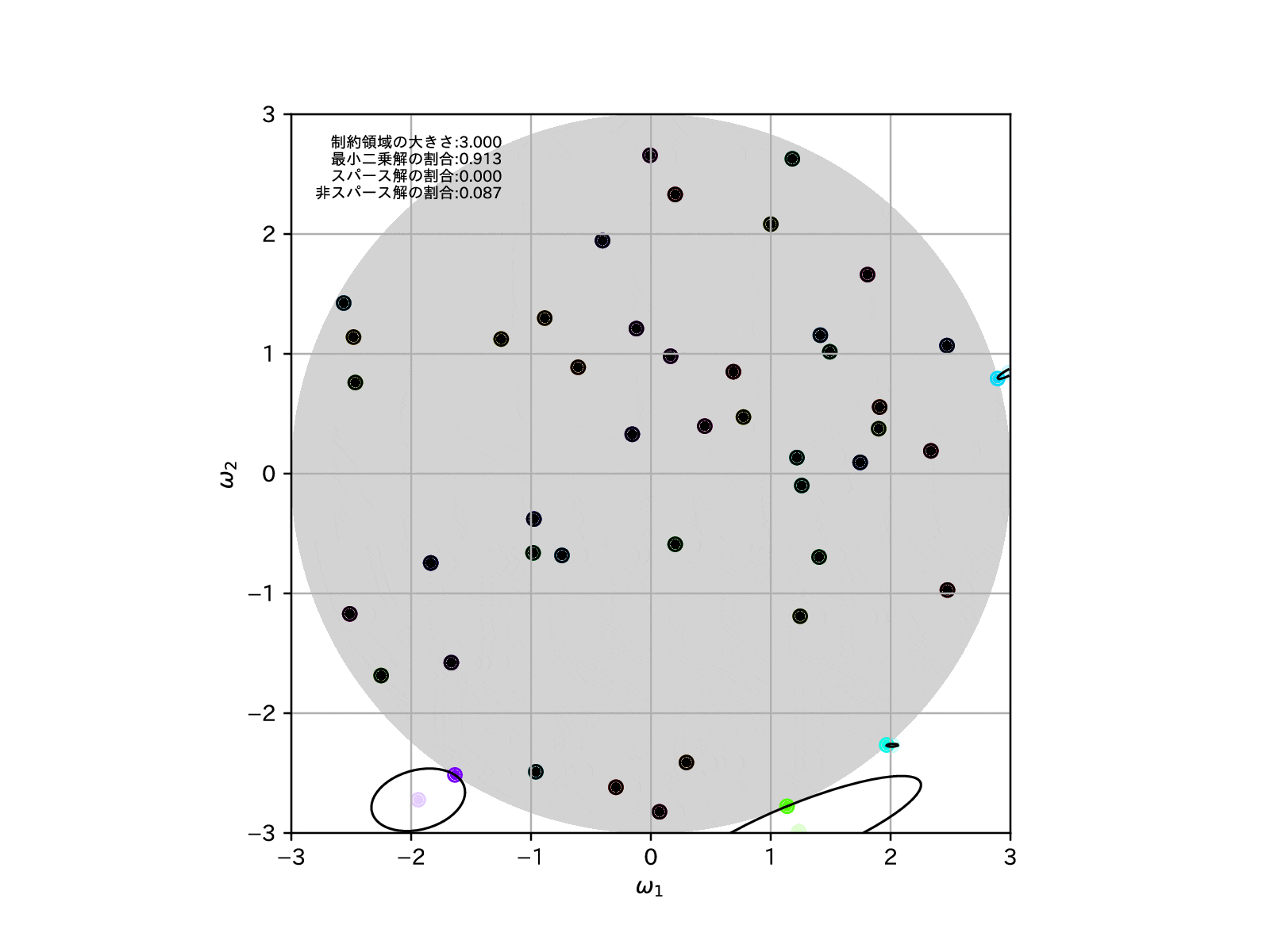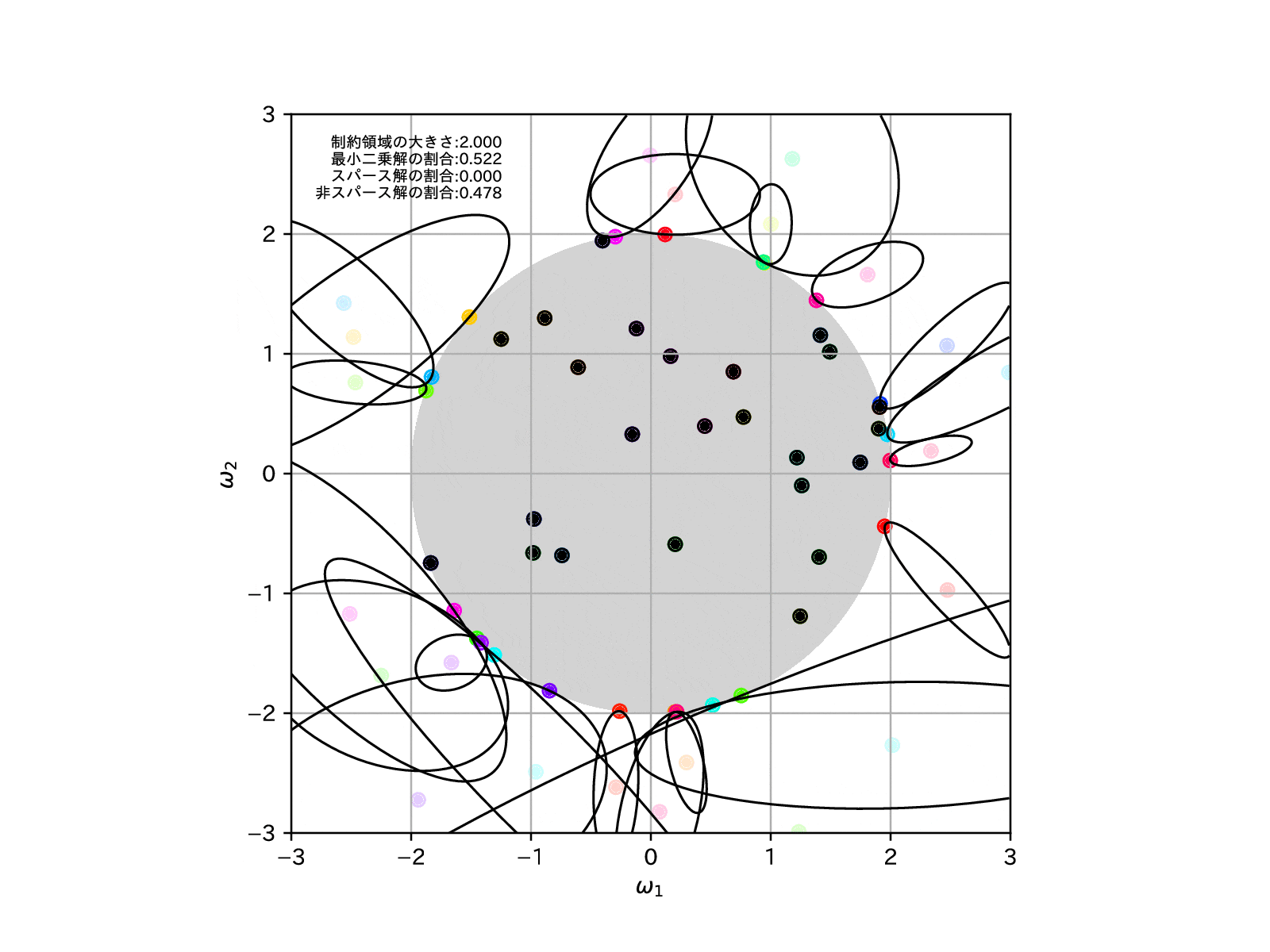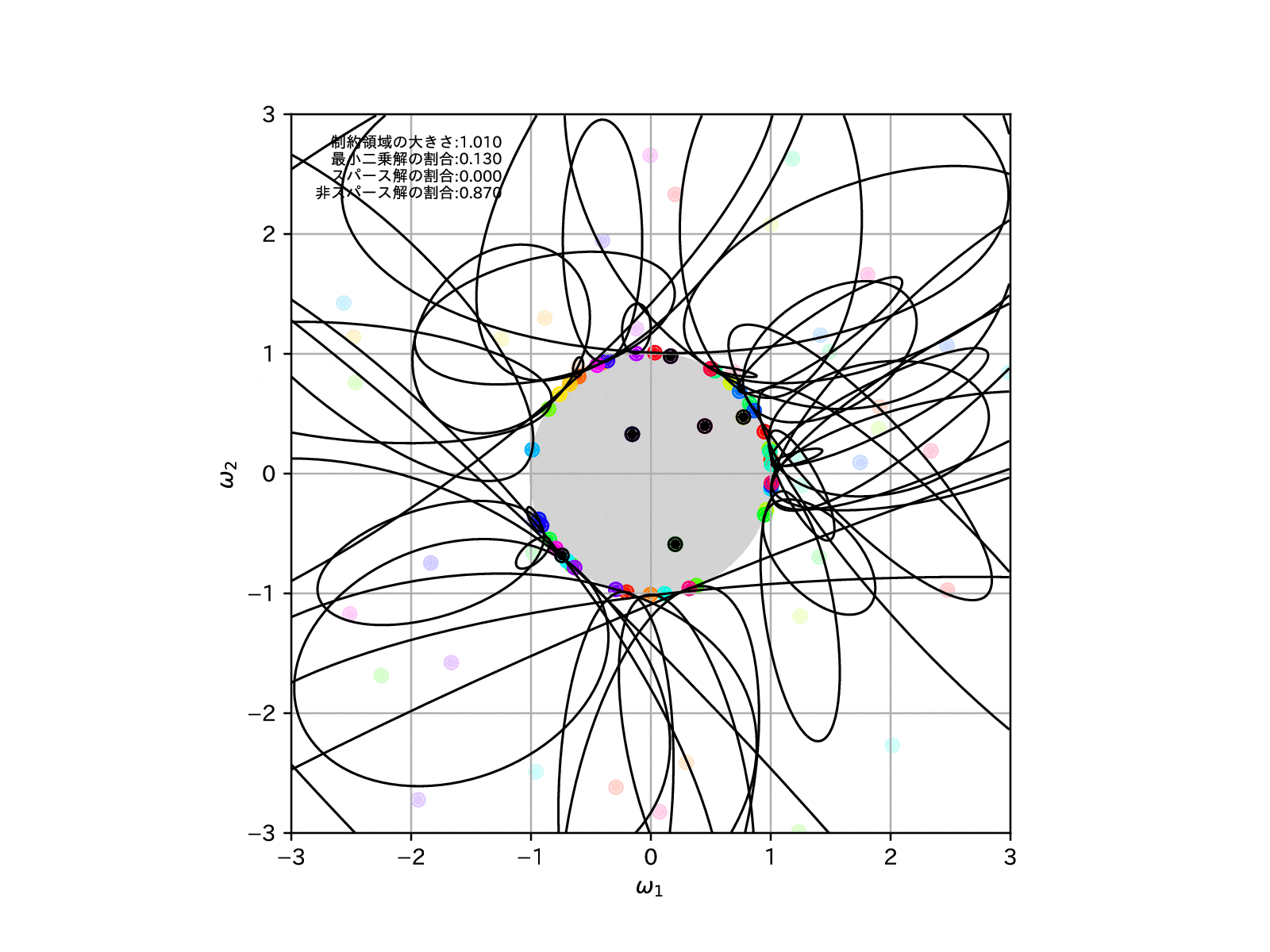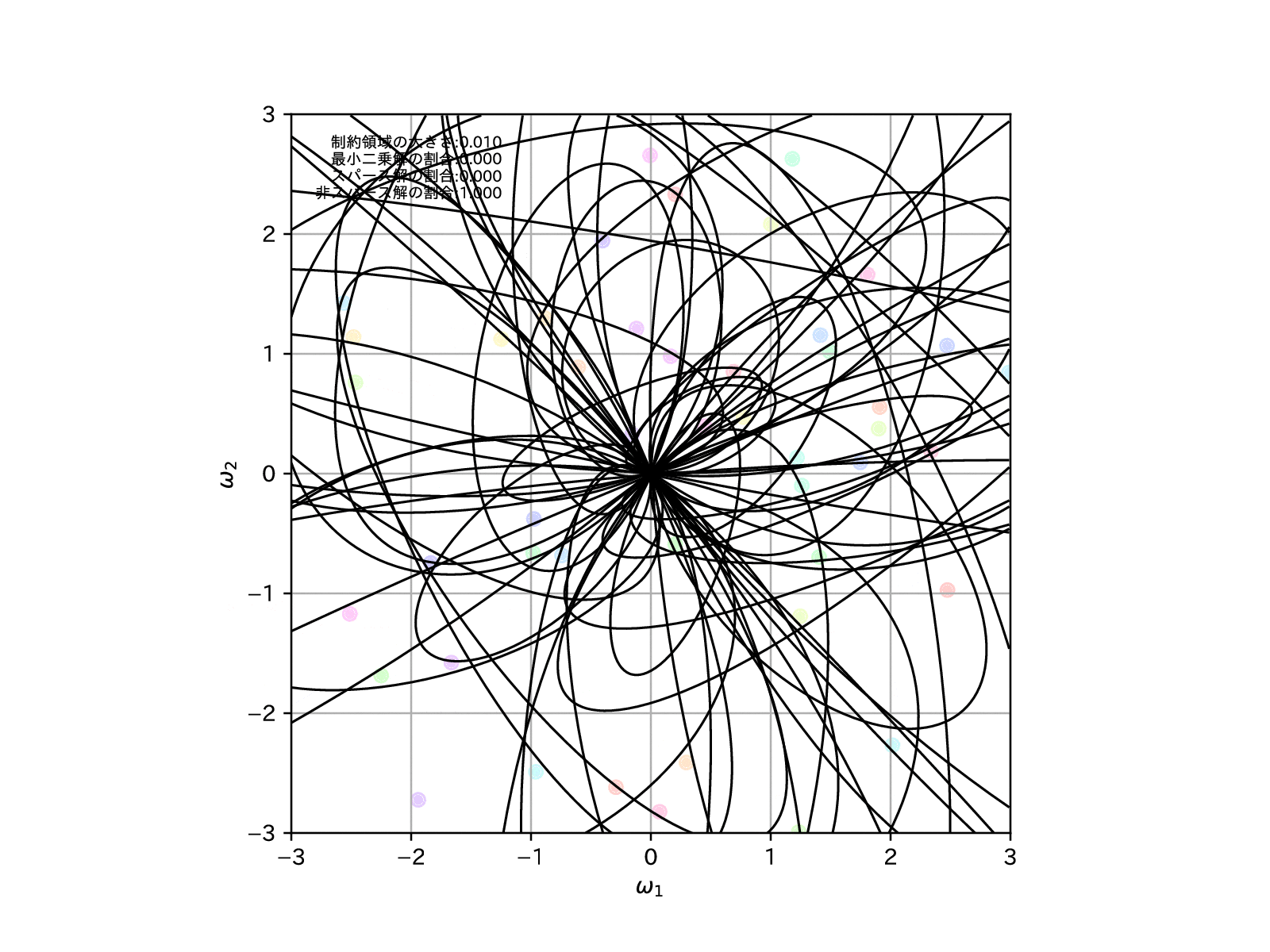
PythonではRIDGE回帰をお手軽に行うために sklearn.linear_model に Ridge クラスおよび RidgeCV クラスが用意されています。
RidgeCV クラスではハイパーパラメータである正則化係数\(\alpha\)のチューニングを交差検証で適当に行い、ベストなものを抽出してくれるので便利です。

from sklearn.linear_model import RidgeCV

alphas = np.logspace(-3, 3, 100)

RidgeCV_model = RidgeCV(alphas=alphas * len(y_train_lmns) / 2)
RidgeCV_model.fit(X_train_lmns_flat, y_train_lmns)
score_L2 = score(y_validation_lmns, X_validation_lmns_flat @ RidgeCV_model.coef_.T)

MAE	: 0.415242871170996
RMSE	: 0.5231652705985934
CORR	: 0.853426886073745
R2	: 0.7266160815053557

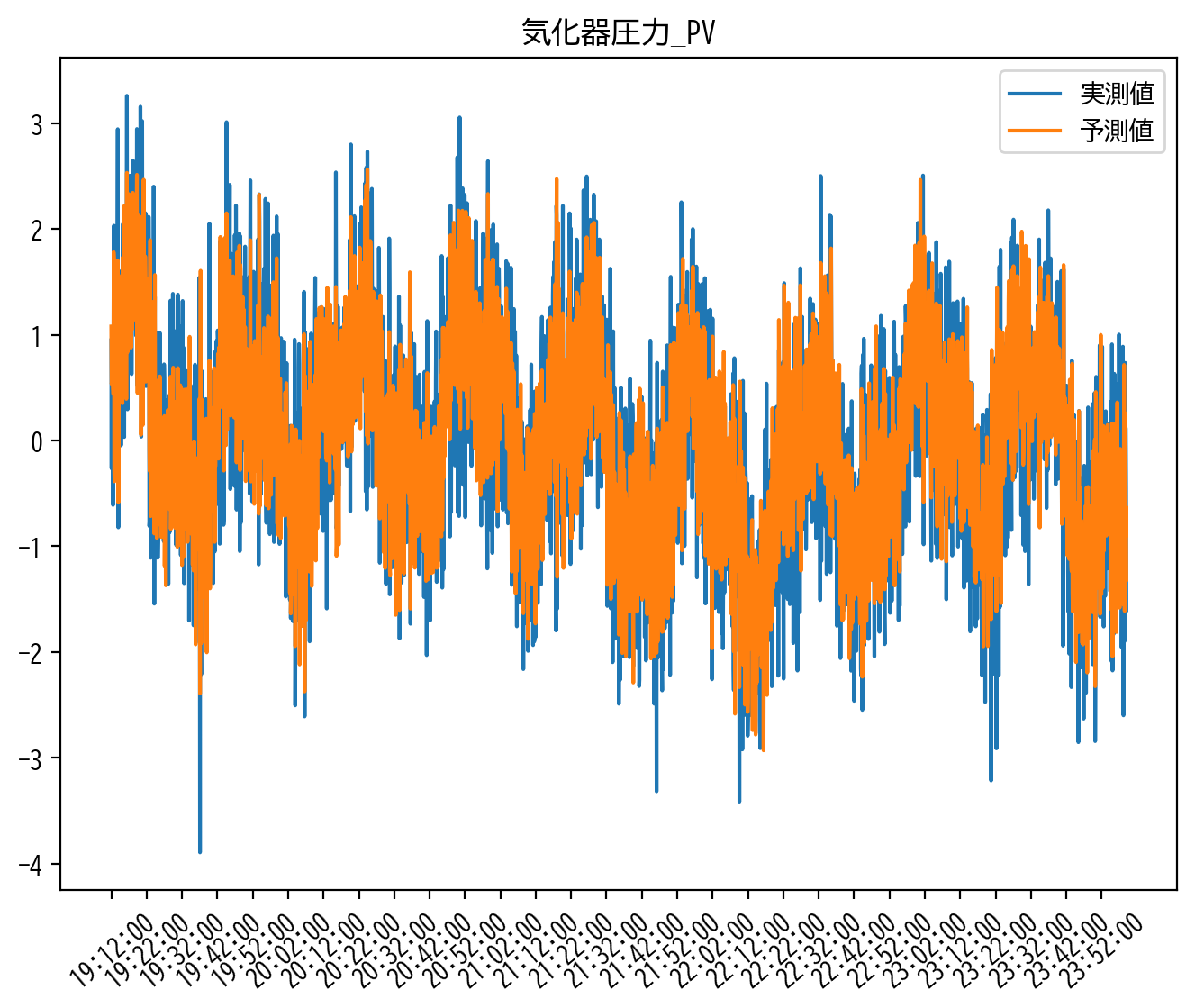
heatmap(RidgeCV_model.coef_)

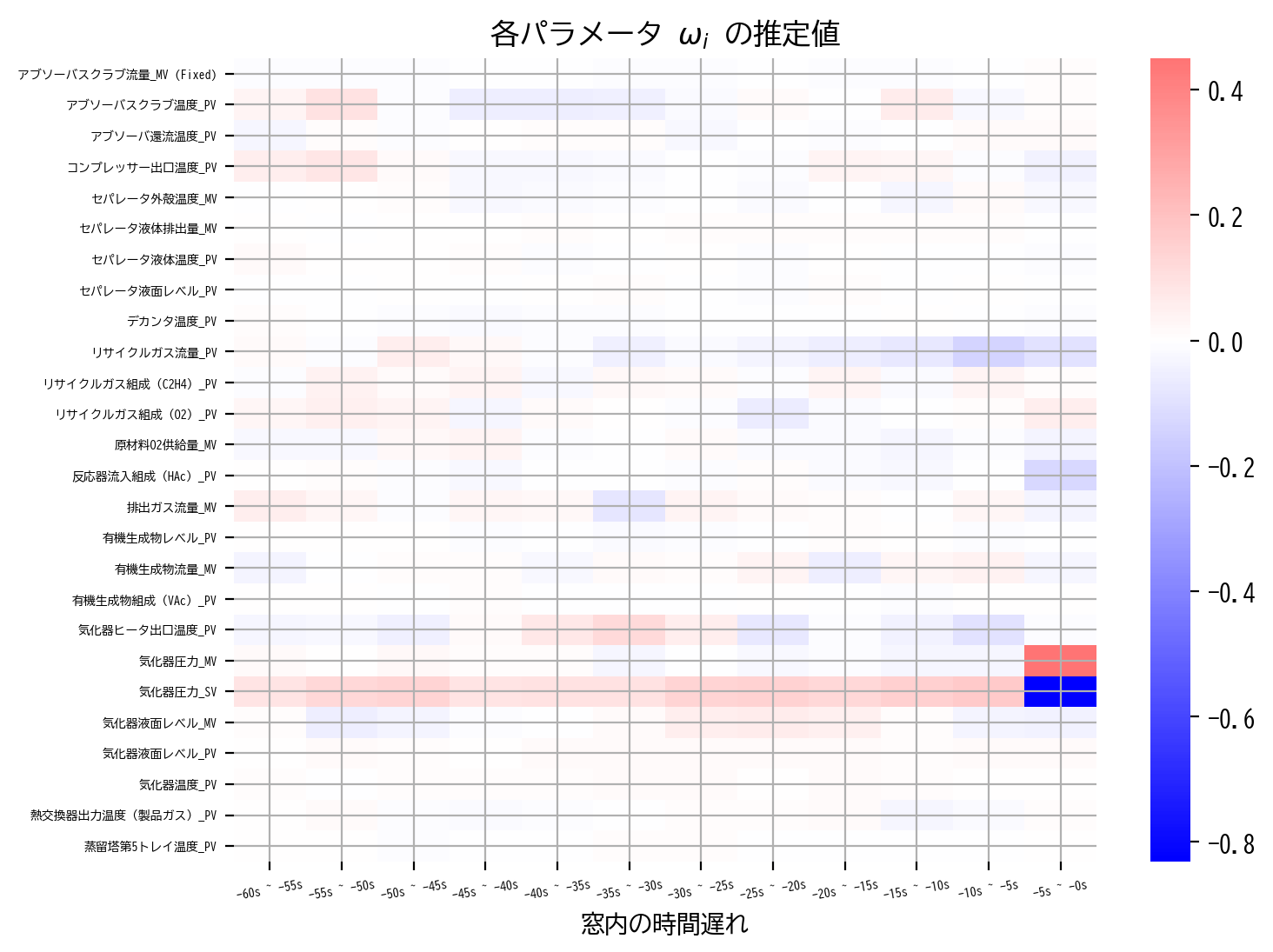
heatmap(RidgeCV_model.coef_, scale=0.5)

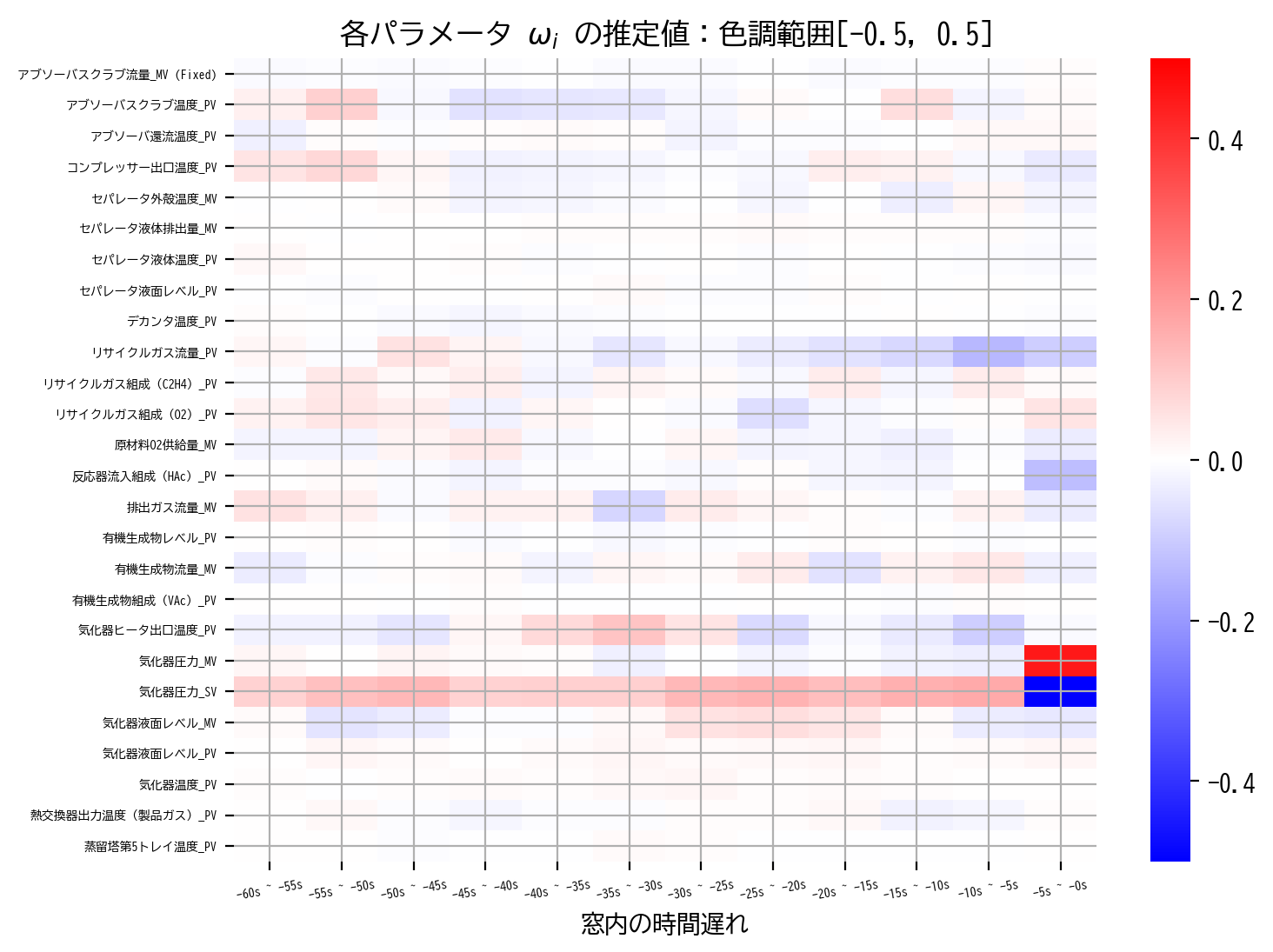
先ほどの最小二乗法の推定結果と比較すると、窓方向の正負変化は抑えられ、滑らかに推定解が変化していることが読み取れます。
すなわち、RIDGE回帰で過学習が抑制され、結果的に多重共線性も抑えられたのではないかと考えることができます。
最後にRIDGE回帰について、各正則化係数\(\alpha\)に応じたパラメータの推定解の挙動を図示してみます。

from sklearn.linear_model import Ridge

coefs = (
    Ridge(alpha=alphas * len(y_train_lmns) / 2)
    .fit(X_train_lmns_flat, np.repeat(y_train_lmns, len(alphas), axis=1))
    .coef_.T[None, :, :]
)
path(alphas, coefs, RidgeCV_model.alpha_ / len(y_train_lmns) * 2)

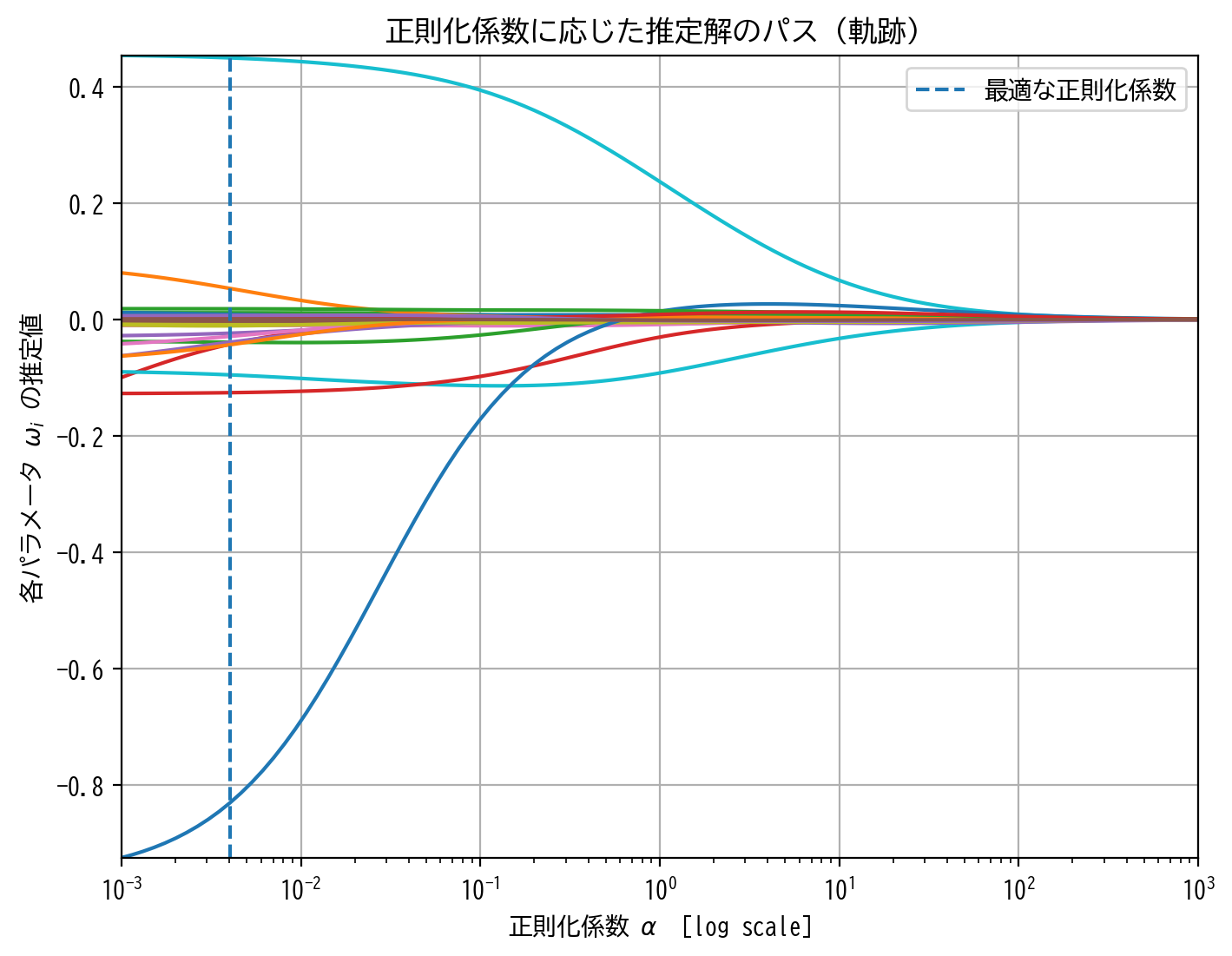
正則化項の影響が強くなる（\(\alpha\to\infty\)）につれて、各パラメータの推定解は滑らかに0に縮小していくことが読み取れます。

LASSO

ここまでの流れを踏まえ、いよいよ最も基本的なスパースモデリングであるLASSO回帰について見てみます。
すでに少し紹介しましたが、LASSO回帰では以下の最適化問題を考えています。

\[ \min_{\omega}\frac{1}{2N}\|y-X\omega\|_2^2+\alpha\|\omega\|_1 \]

すなわち、軸上に頂点があるような正方形が制約領域となります。
LASSOのようなスパースモデリングでは、滑らかでない点（微分不可能な点）で最適解となりやすいことを利用してスパースな解を得ていました。
このことを以下の図を用いて確認してみます。
以下ではRIDGE回帰で使用したものと同様の最適化問題を用意し、制約領域のみLASSO回帰のものを使用しています。
この図では薄い点が最小二乗解を、濃い点が対応するLASSO回帰解を示していることに注意してください。

x, y = sympy.symbols("x y", real=True)
Omega_L1 = sympy.Abs(x) + sympy.Abs(y) - 1
image(Omega_L1)

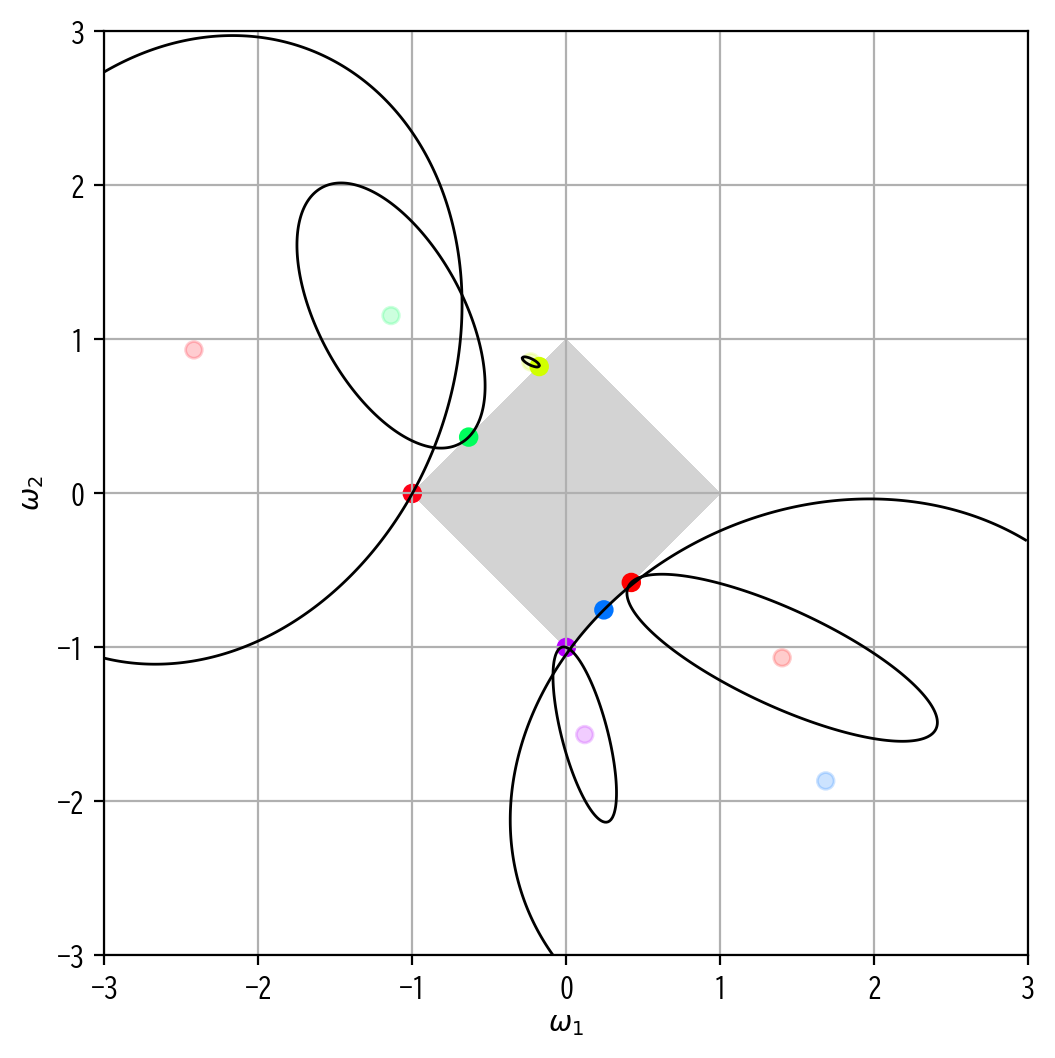
このLASSO回帰の図をみると、RIDGE回帰ではなかった特徴として、最適解がスパースな解となっている学習モデルがいくつか存在することがわかります。
例えば\((\omega_1,\omega_2)=(-1,0)\)となっている赤点や、\((\omega_1,\omega_2)=(0,-1)\)となっている紫点などが見て取れます。
さらにイメージできることとして、正則化係数を大きくし制約領域をさらに縮めていけば、最適解がスパースな解となる学習モデルが増えていく気がします。
このことを確認するために、先ほどと同様に学習モデルを100個用意して、この制約領域を縮めていったとき、すなわち\(\alpha\to\infty\)とした場合の、パラメータの推定解の挙動を示してみます。

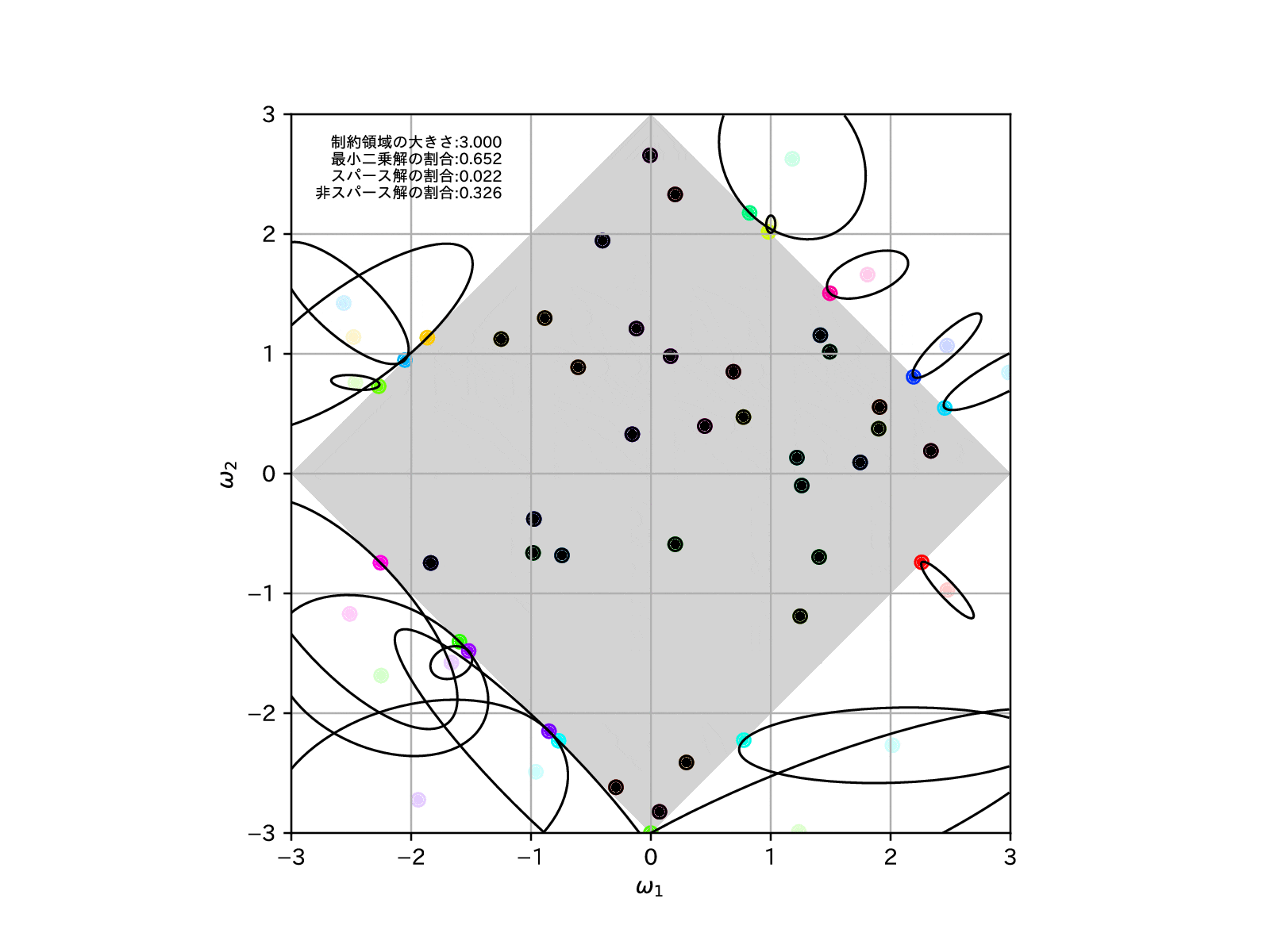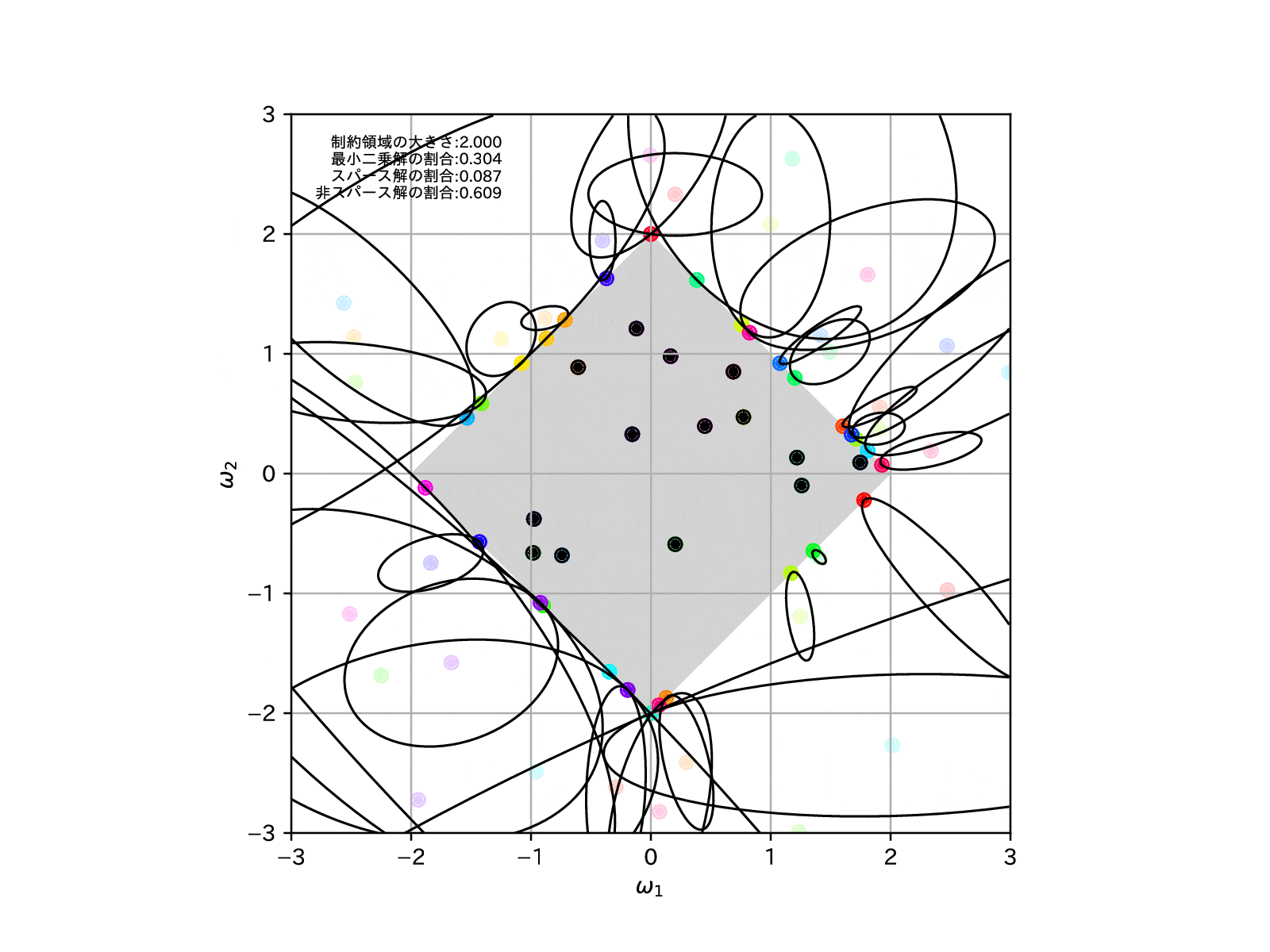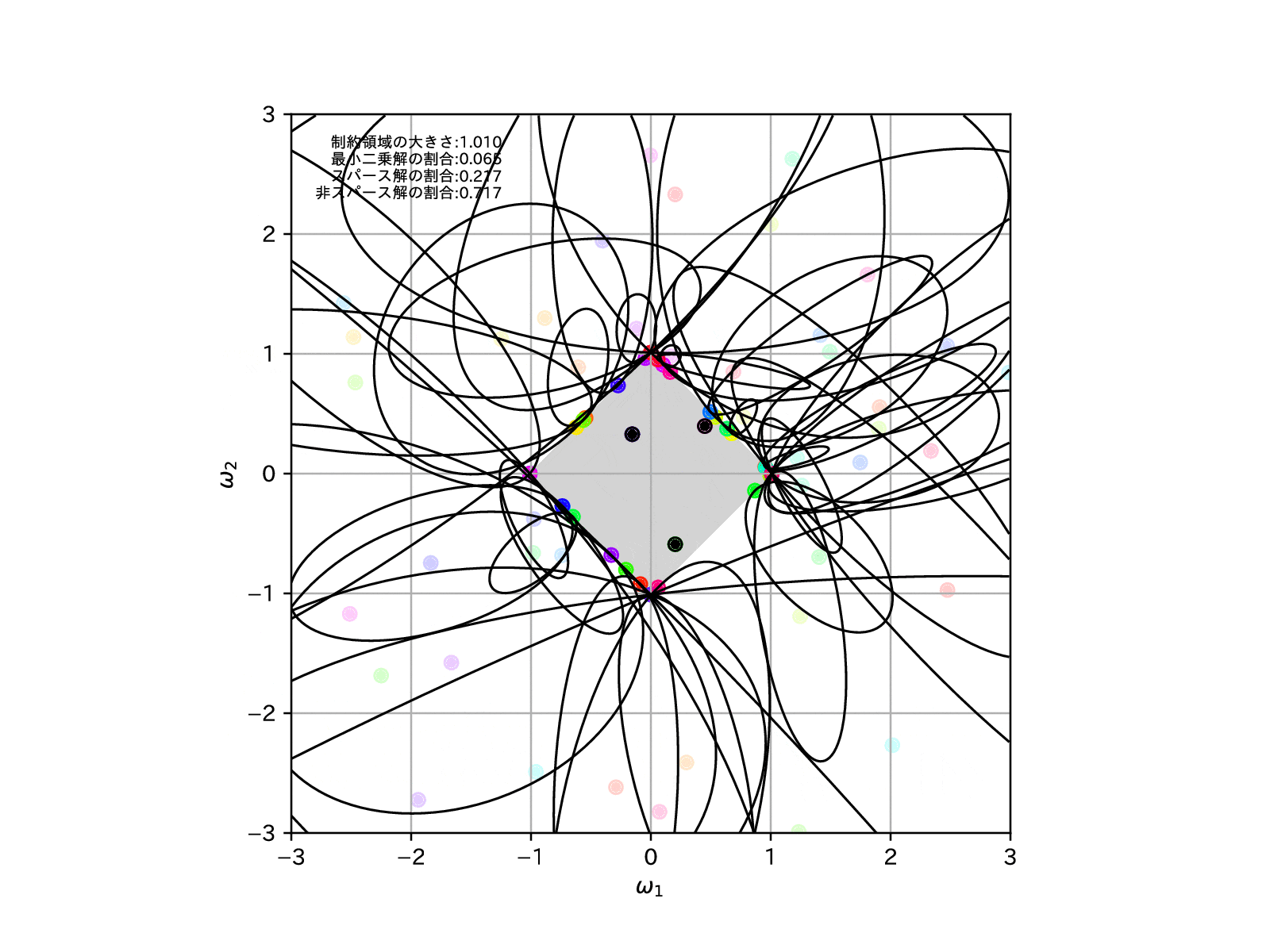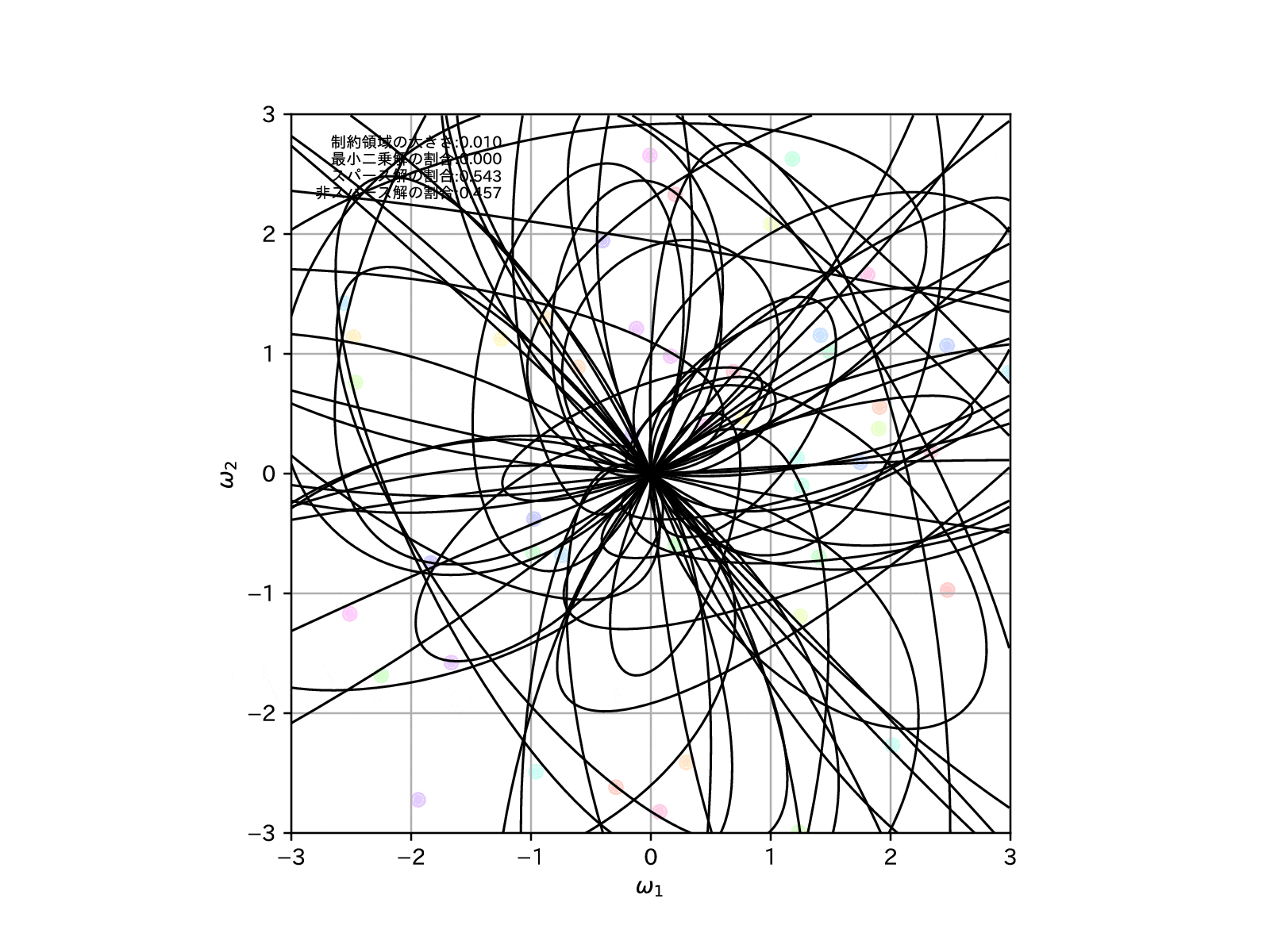
全学習モデルのうち、最適解がスパースな解となったものの割合を左上に示しています。
これを見ると、確かに制約領域を縮めていけばいくほど、最適解がスパースな解となりやすくなっていることが確認することができます。
PythonではLASSO回帰をお手軽に行うために sklearn.linear_model に Lasso クラスおよび LassoCV クラスが用意されています。
特に LassoCV クラスでは、RidgeCV クラスと同様、ハイパーパラメータである正則化係数\(\alpha\)のチューニングを交差検証で適当に行い、ベストなものを抽出してくれるので便利です。

from sklearn.linear_model import LassoCV

LassoCV_model = LassoCV(n_jobs=-1)
LassoCV_model.fit(X_train_lmns_flat, y_train_lmns)
score_L1 = score(y_validation_lmns, X_validation_lmns_flat @ LassoCV_model.coef_.T)

MAE	: 0.4054973873738526
RMSE	: 0.5109616894770228
CORR	: 0.8601387631618306
R2	: 0.739221472006576

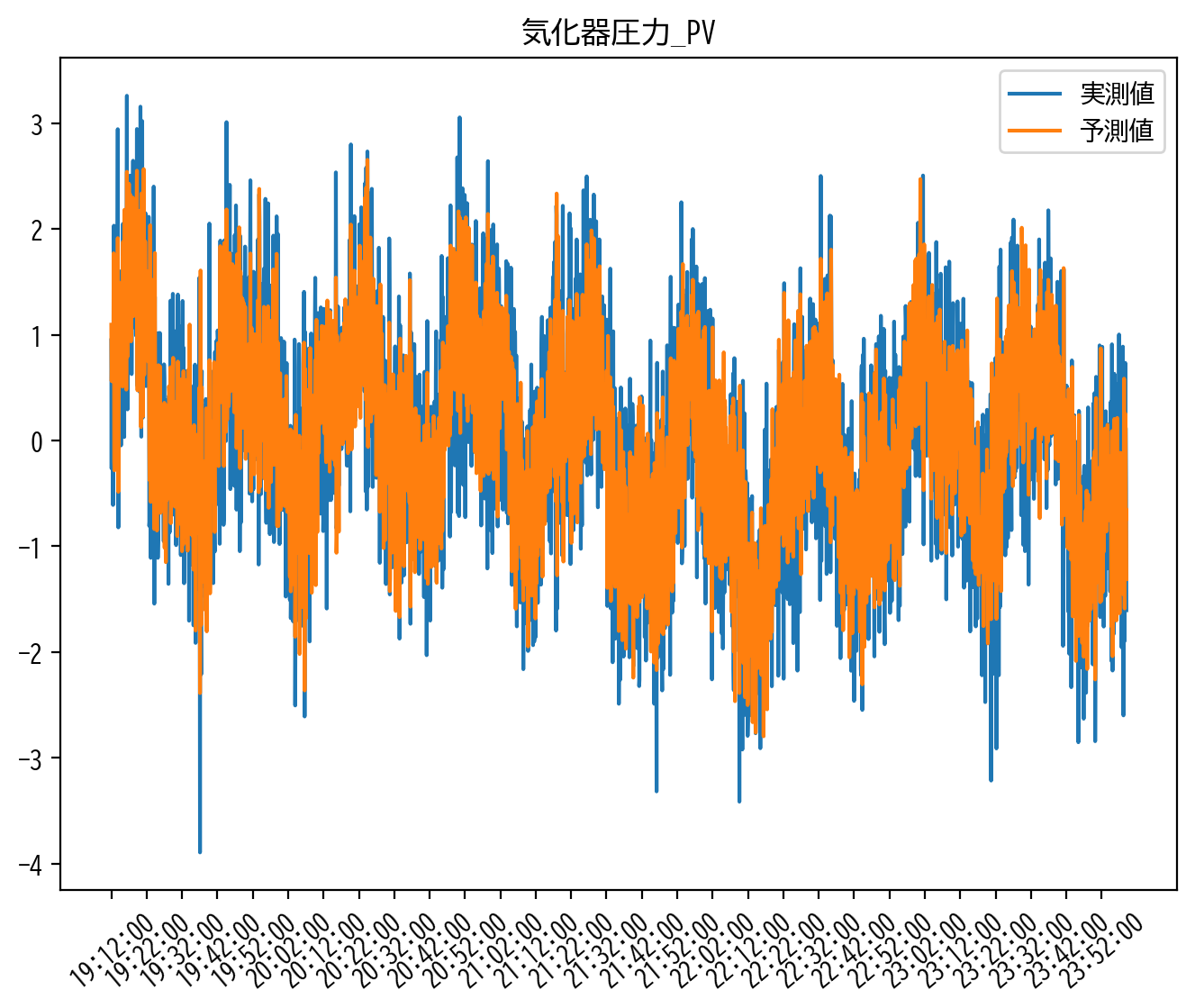
heatmap(LassoCV_model.coef_)

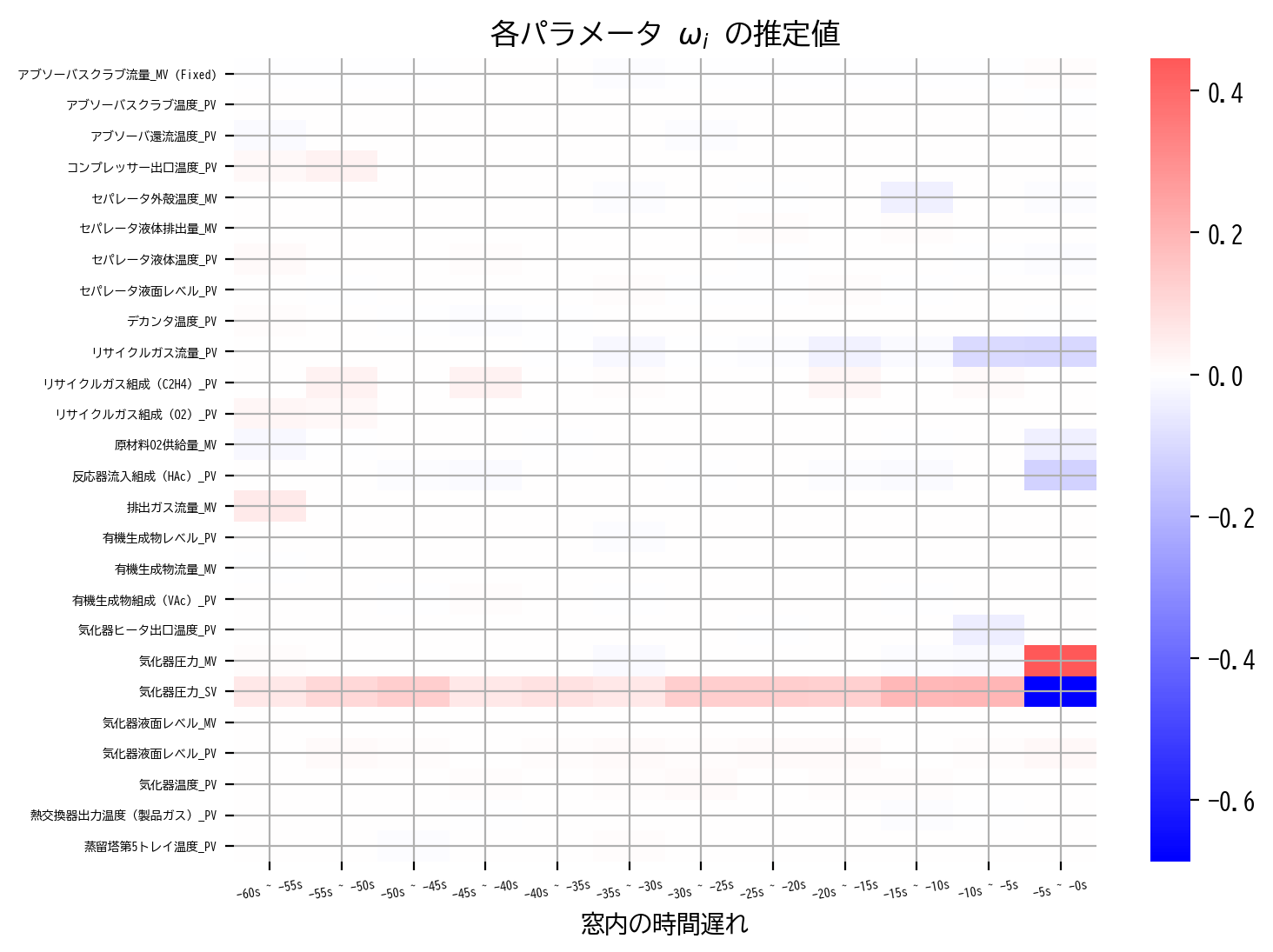
heatmap(LassoCV_model.coef_, scale=0.5)

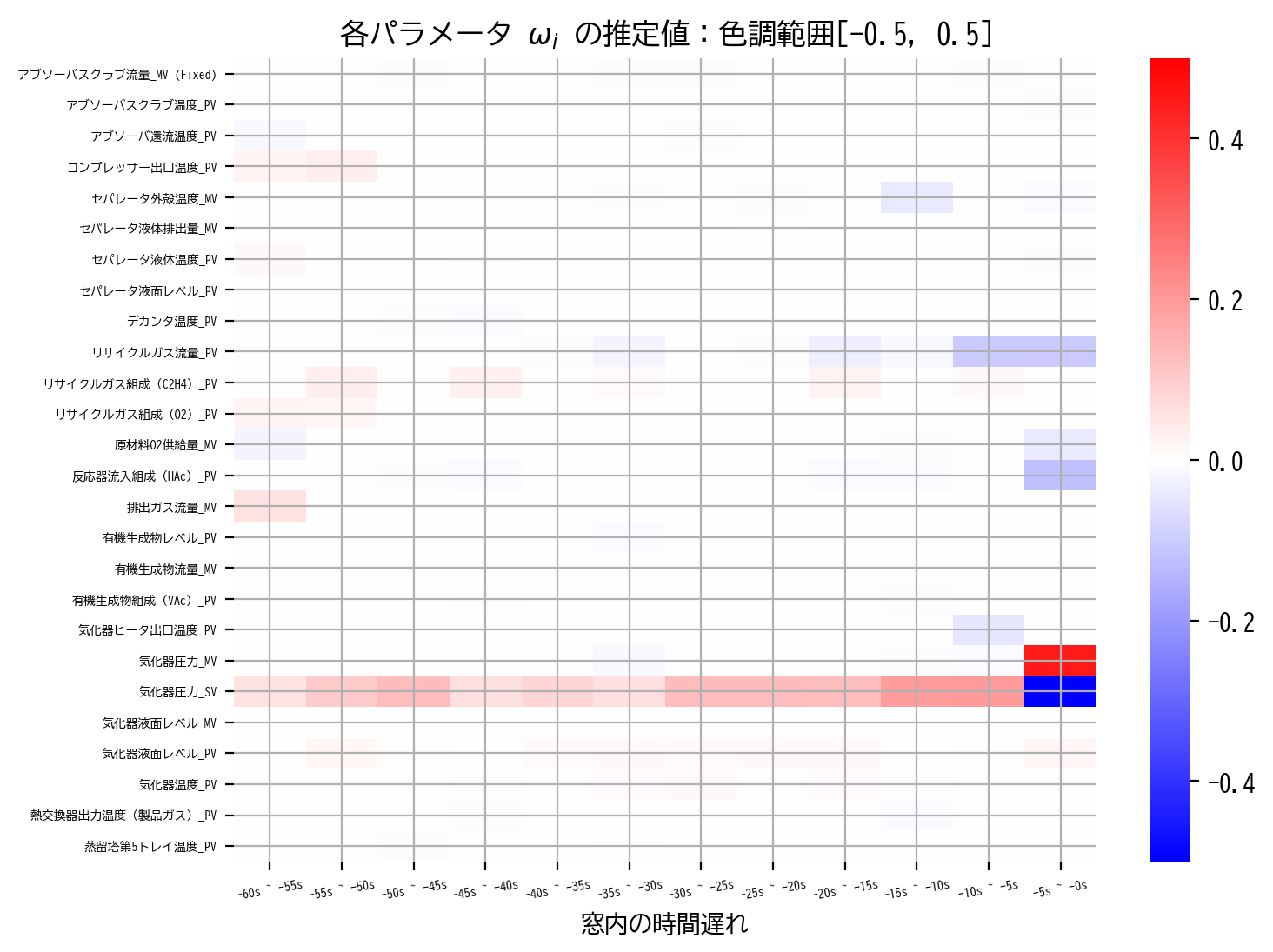
最小二乗法の推定結果やRIDGE回帰の推定結果と比較すると、それまで滑らかだった窓方向の推定解の変化が、明らかにスパースになっていることが見て取れます。
すなわち、LASSO回帰では、目的変数に本質的に影響を与えないパラメータを0に推定することで過学習を抑制し、結果的に多重共線性についても抑えたような推定解が得られたと考えることができます。
しかし、LASSO回帰にもいくつかデメリットがあります。
例えば、以下の様に正則化係数に応じた推定解のパスを図示すると、問題点が表出します。

from sklearn.linear_model import lasso_path

alphas, coefs, _ = lasso_path(X_train_lmns_flat, y_train_lmns)
path(alphas, coefs, LassoCV_model.alpha_)

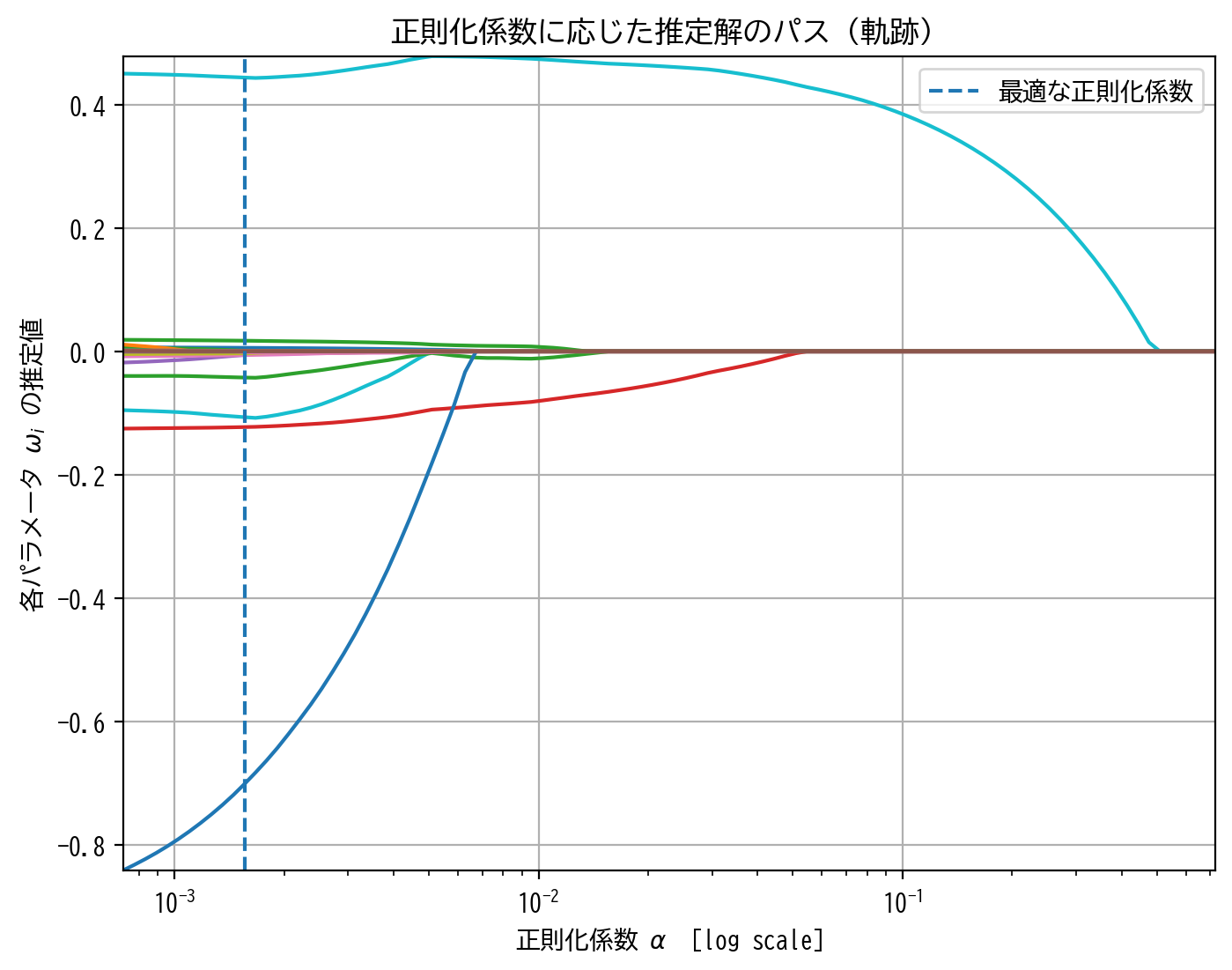
正則化係数の増大に対して、RIDGE回帰ではほとんどのパラメータは滑らかに0に縮小していきました。
しかし、LASSO回帰では必ずしもそうとは言い切れず、正則化係数の増大の過程で、カクカクと折れ曲がったり、パラメータが0から遠ざかったり、大小関係が入れ替わったり、一旦0と推定されたのに再度非0に戻ってきたりと、端的にまとめれば推定解に一貫性や一致性がないような気がします。
このような現象について、LASSO回帰には「変数選択の一致性」がないと言ったりします。

Elastic Net

冒頭でも少し触れた様に、スパースモデリングは正則化項\(\Omega(\omega)\)の構造を変化させることで、さまざまなアレンジを行うことができます。
ここで紹介するElastic Netは、最もよく見るアレンジのひとつです。
具体的には以下のような最適化問題を解くことを考えます。

\[ \min_{\omega}\frac{1}{2N}\|y-X\omega\|_2^2+\alpha\left(r\|\omega\|_1+\frac{1-r}{2}\|\omega\|_2^2\right) \]

正則化項の構造から分かる様に、Elastic NetではRIDGE回帰とLASSO回帰をミックスしたような構造を取っています。
実際の挙動のイメージも、後で詳しく確認しますがRIDGE回帰とLASSO回帰の性質をミックスしたものと思って大丈夫でしょう。
なお、Elastic Netでは通常の正則化係数に加え、RIDGE回帰とLASSO回帰の影響力の比を調整するハイパーパラメータ\(r\)が追加されます。
ですので、本来チューニングすべきパラメータは\(\alpha\)と\(r\)の２つになるのですが、ここではElastic Netの性質を確認することが重要だと思いますので、以降\(r=0.5\)、すなわちRIDGE回帰とLASSO回帰は半々の影響を及ぼすElastic Netのみを考え、\(\alpha\)のみチューニングすることとします。
この場合、実際の最適化問題は以下のように図示されます。
この図では薄い点が最小二乗解、濃い点が対応するElastic Net解を示しています。

x, y = sympy.symbols("x y", real=True)
Omega_EN = sympy.Rational(1, 2) * (sympy.Abs(x) + sympy.Abs(y) - 1) + sympy.Rational(
    1, 2
) * (x**2 + y**2 - 1**2)
image(Omega_EN)

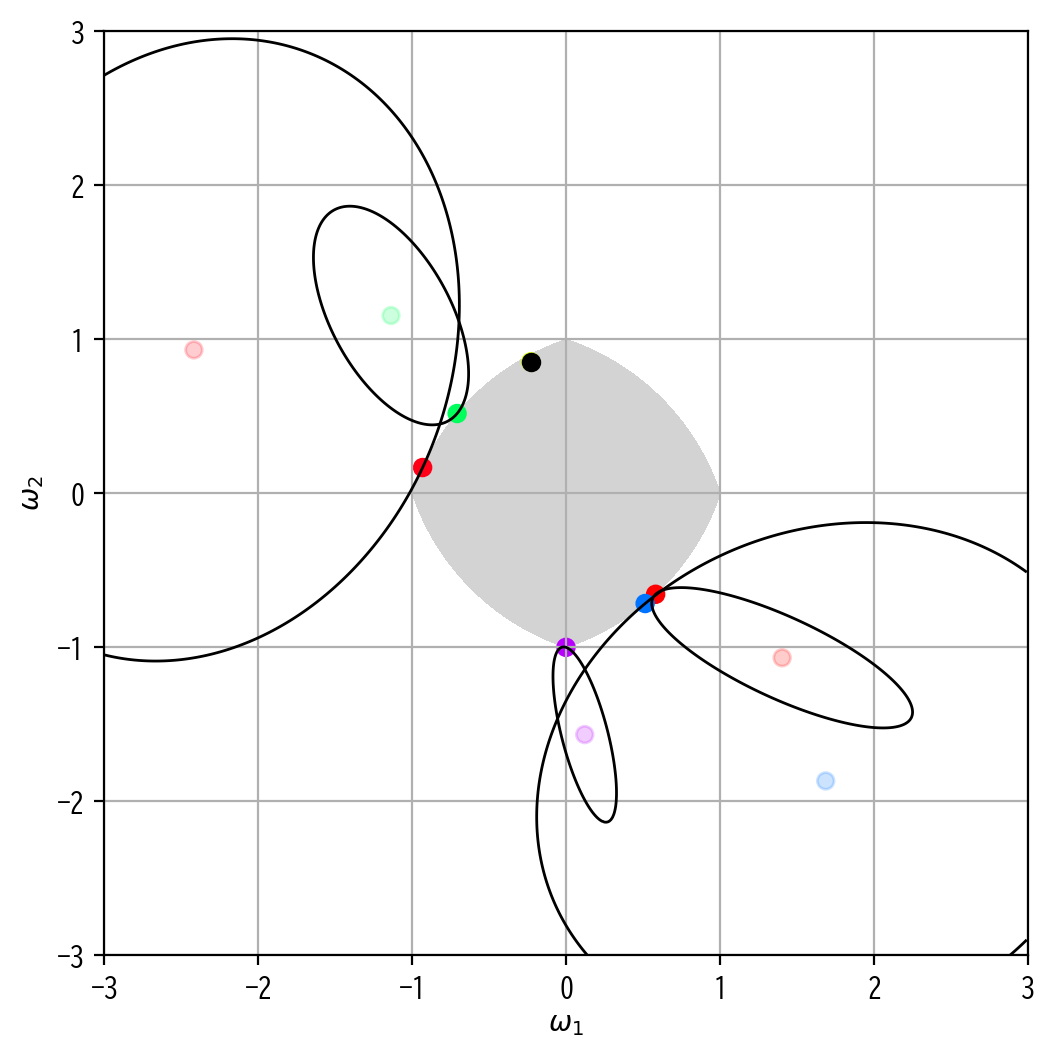
制約領域の形状を確認すると、RIDGE回帰とLASSO回帰をミックスした様な、角がありつつも辺は丸みを帯びている様な、座布団型をしています。
そのため、Elastic NetではLASSO回帰よりもスパースな推定解に誘導する力が抑えられている分、RIDGE回帰のような安定した縮小推定を行うことが可能なのです。
同じく例によって、同様の学習モデルを100個用意して、制約領域を縮めていったとき、すなわち\(\alpha\to\infty\)とした場合の、パラメータの推定解の挙動を確認してみます。

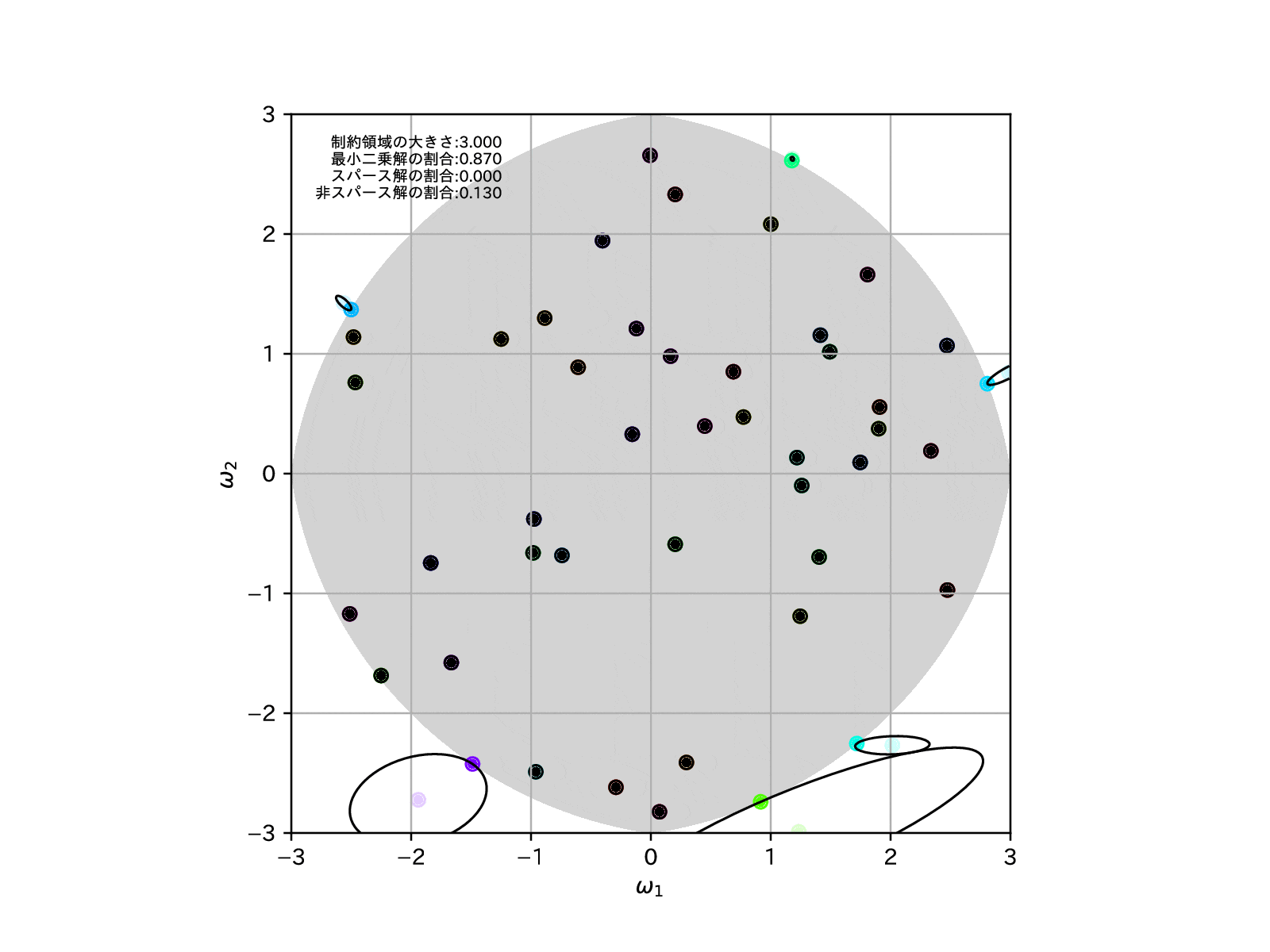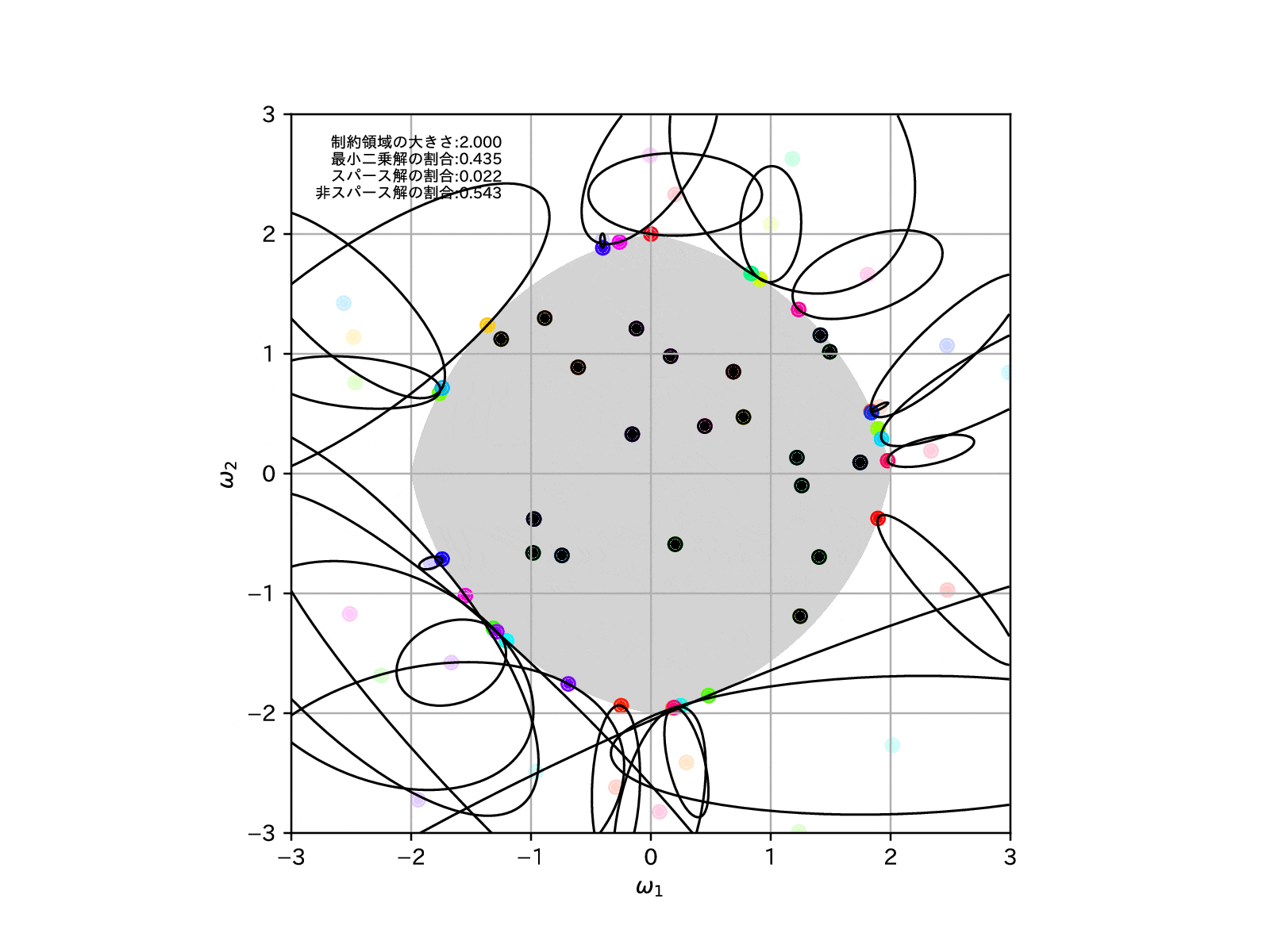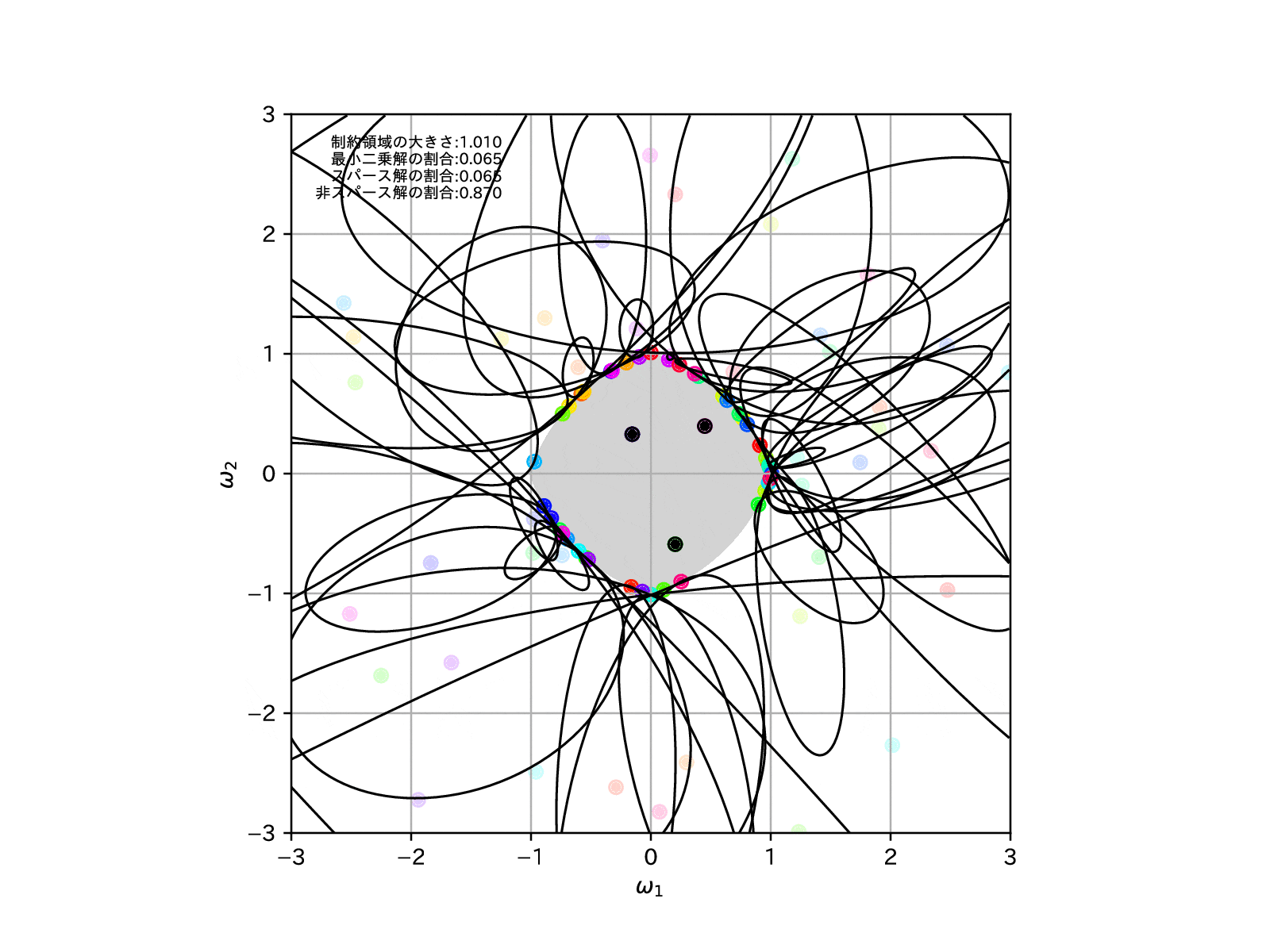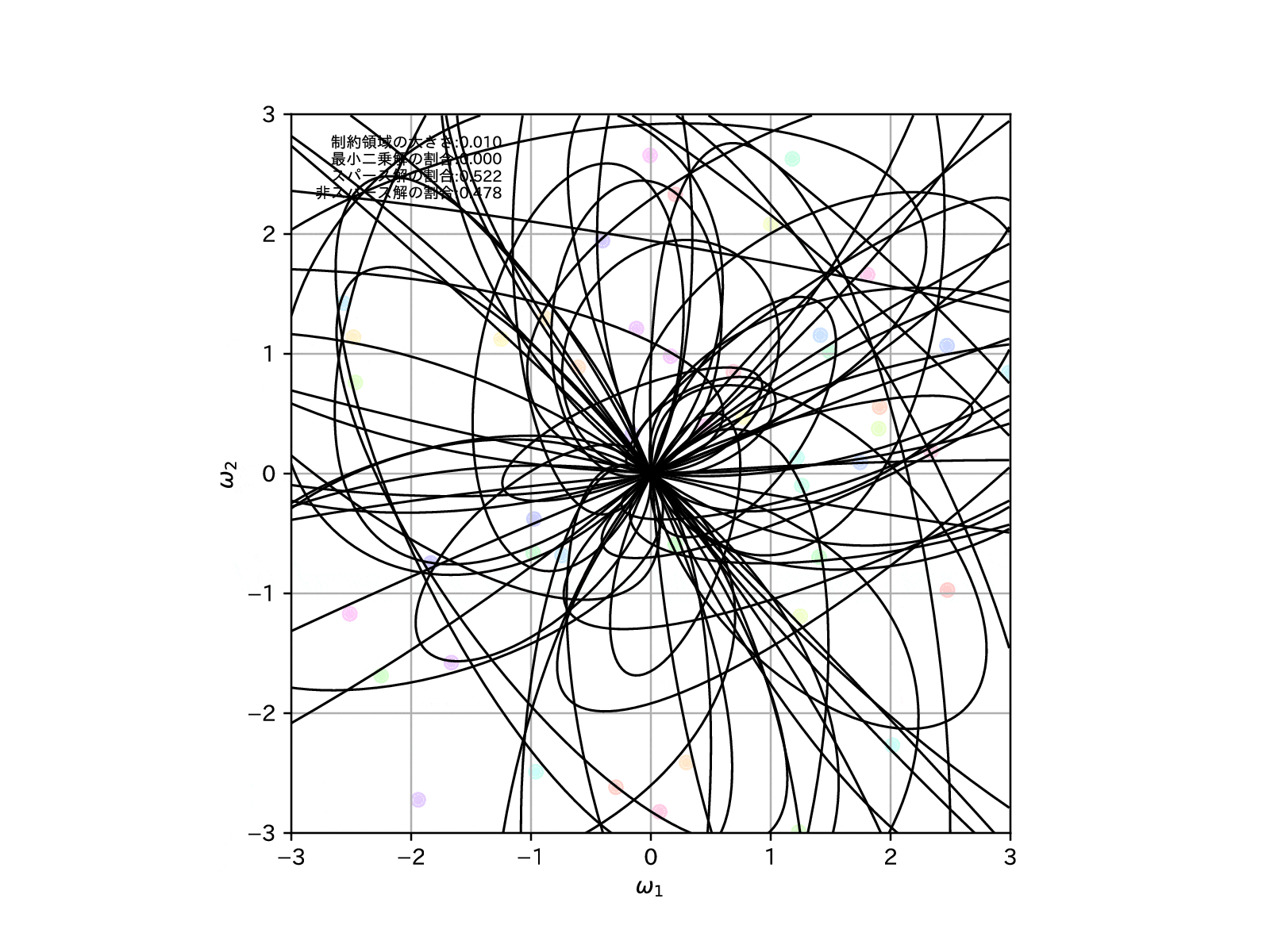
LASSO回帰よりもスパース解の割合は増えませんが、より直線的に0に縮小推定できているように読み取れます。
PythonではElastic Net回帰をお手軽に行うために、例によって sklearn.linear_model に ElasticNet クラスおよび ElasticNetCV クラスが用意されています。
特に ElasticNetCV クラスでは、RidgeCV クラスや LassoCV クラスと同様、ハイパーパラメータである正則化係数\(\alpha\)のチューニングを交差検証で適当に行い、ベストなものを抽出してくれるので便利です。
ただし、RIDGE回帰とLASSO回帰の影響力の比を調整するハイパーパラメータ\(r\)については、事前に交差検証に用いる候補を与える必要があるようです。
何も与えなかった場合は\(r=0.5\)として\(\alpha\)についてのみ交差検証する様ですので、ここでは特に指定しないこととします。
詳しくは scikit-learn の公式ドキュメントを参照してください。

from sklearn.linear_model import ElasticNetCV

ElasticNetCV_model = ElasticNetCV(n_jobs=-1)
ElasticNetCV_model.fit(X_train_lmns_flat, y_train_lmns)
score_EN = score(y_validation_lmns, X_validation_lmns_flat @ ElasticNetCV_model.coef_.T)

MAE	: 0.4066533290929123
RMSE	: 0.51242889630149
CORR	: 0.8593272120743953
R2	: 0.7377216908000874

heatmap(ElasticNetCV_model.coef_)

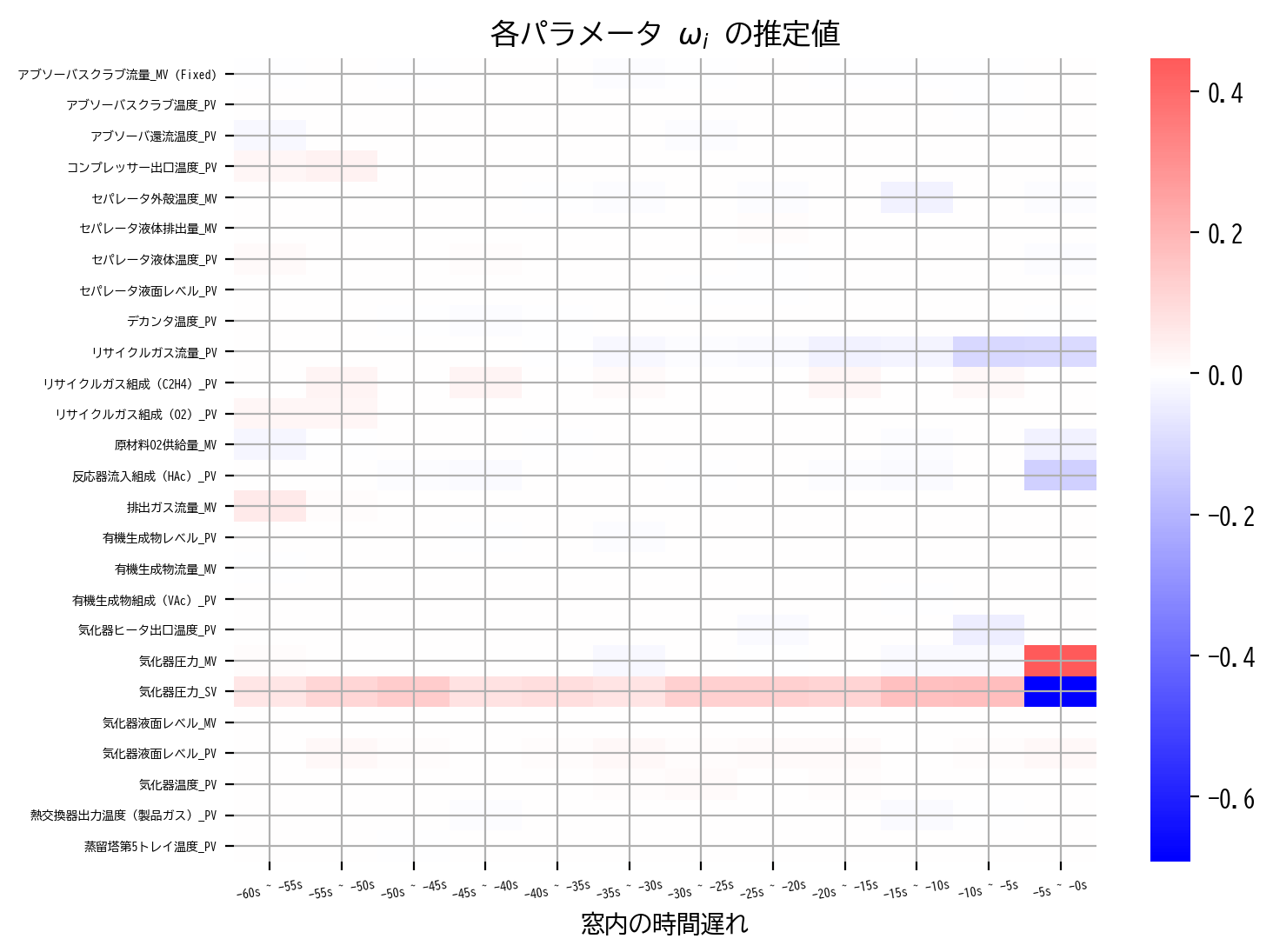
heatmap(ElasticNetCV_model.coef_, scale=0.5)

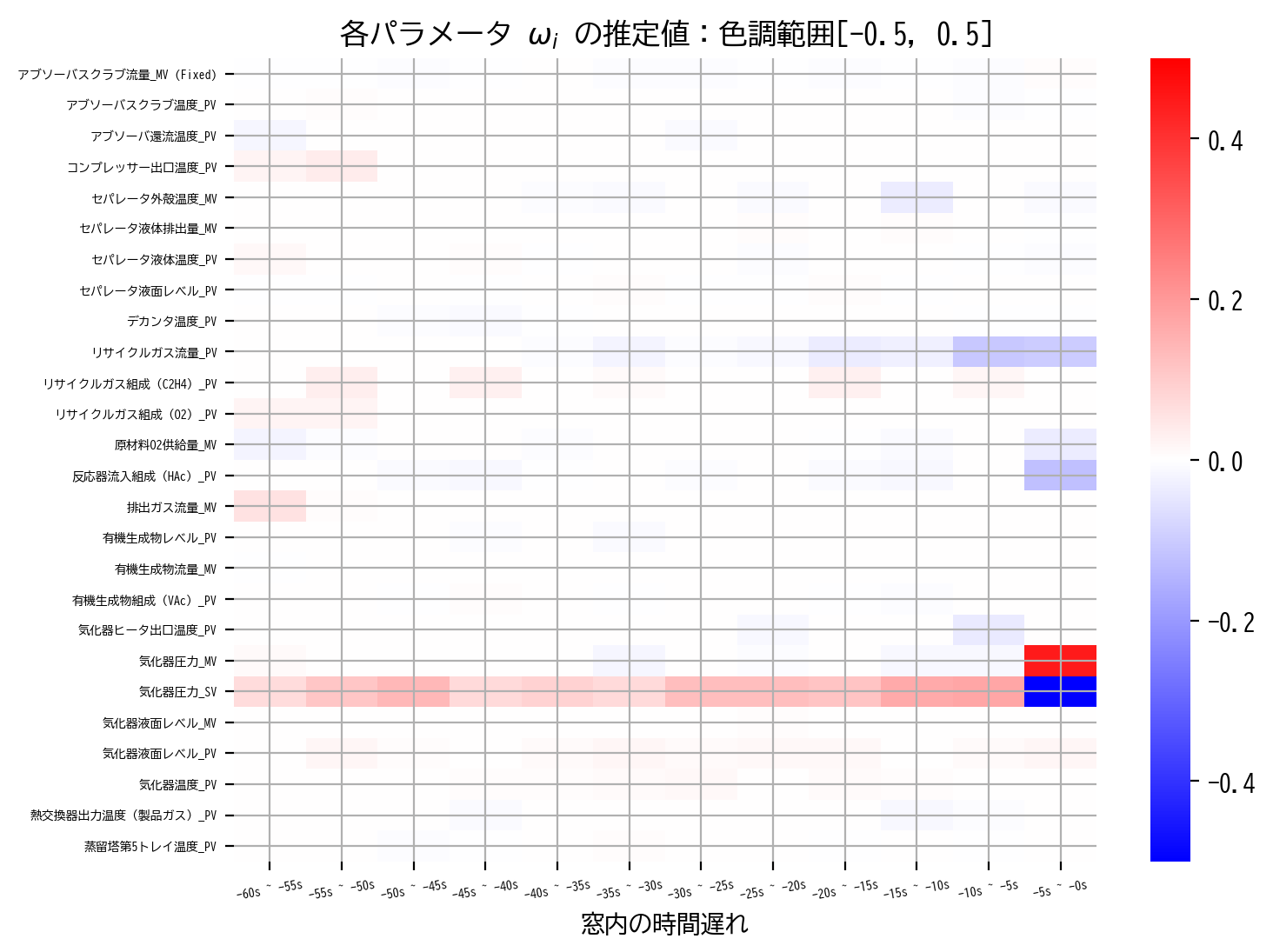
RIDGE回帰とLASSO回帰のイイトコ取りした推定解が得られていると思います。
（もはや主観に訴えかけるしかないので、ここでは雑な感想で留めることとします。）
同様にElastic Netについて、各正則化係数\(\alpha\)に応じたパラメータの推定解の挙動を確認してみます。

from sklearn.linear_model import enet_path

alphas, coefs, _ = enet_path(X_train_lmns_flat, y_train_lmns)
path(alphas, coefs, ElasticNetCV_model.alpha_)

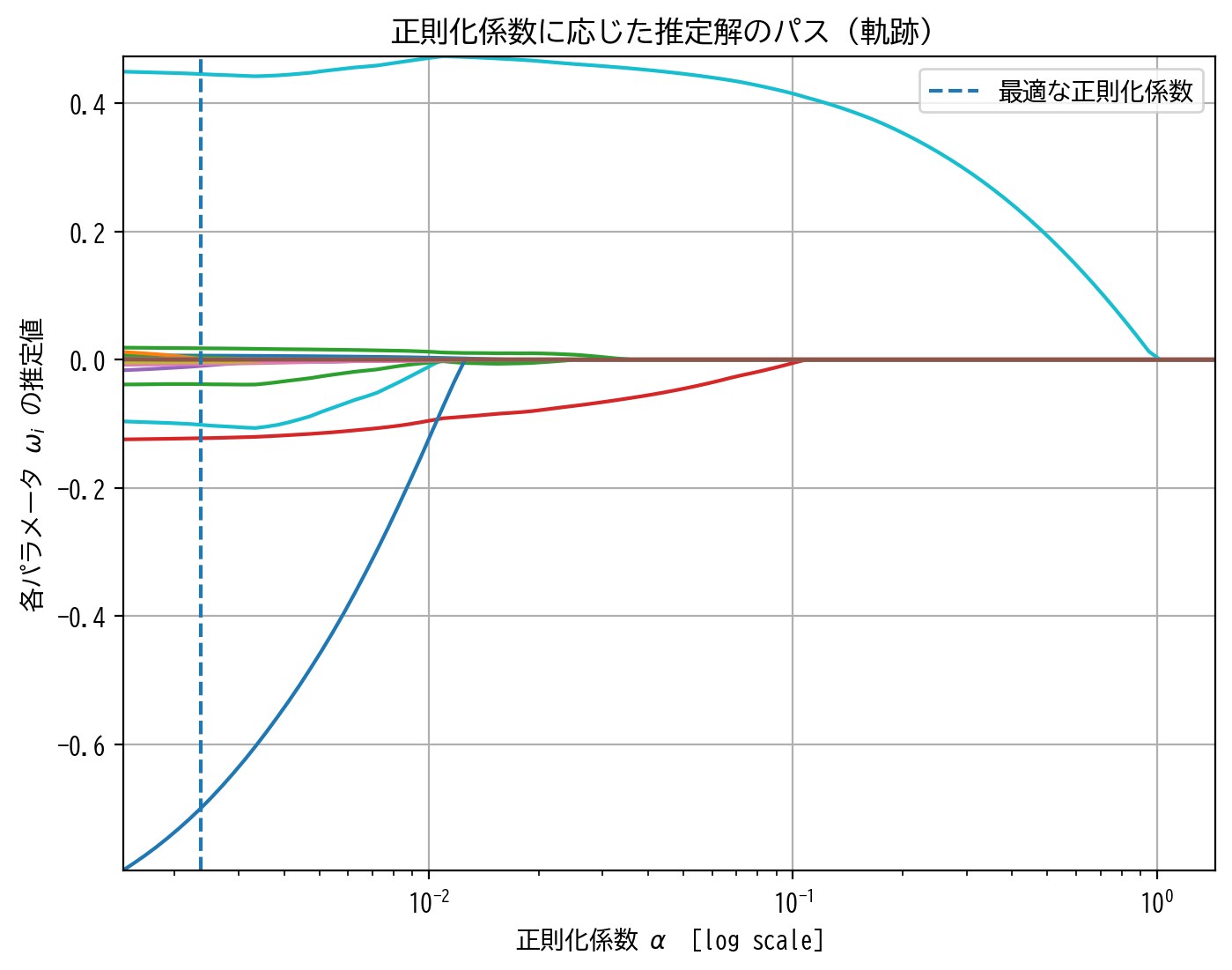
先ほどLASSO回帰でみられたような、推定解の挙動の不安定さは多少軽減されたような気がしないでもないでしょうか。
それでいて、スパースな解も得られているので実用上はElastic Netが優っているかもしれません。

各手法の比較

最後に今回取り扱った学習手法の、検証データに対する推定結果（推定精度）をまとめます。
（本当は検証データとテストデータを分けた方が良いので参考程度に確認してください。）

result = pd.concat([score_LR, score_L2, score_L1, score_EN])
result.index = ["Least Square Method", "RIDGE", "LASSO", "Elastic Net"]
result

	mae	rmse	corr	r2
Least Square Method	0.453843	0.573583	0.825699	0.671385
RIDGE	0.415243	0.523165	0.853427	0.726616
LASSO	0.405497	0.510962	0.860139	0.739221
Elastic Net	0.406653	0.512429	0.859327	0.737722

# 最小値
result.idxmin()

mae                   LASSO
rmse                  LASSO
corr    Least Square Method
r2      Least Square Method
dtype: object

# 最大値
result.idxmax()

mae     Least Square Method
rmse    Least Square Method
corr                  LASSO
r2                    LASSO
dtype: object

MAE（平均絶対誤差）とRMSE（二乗平均平方根誤差）は小さい方が、CORR（相関係数）とR2（決定係数）は大きい方が良いことを考慮すると、本稿では LASSO回帰に総合評価の軍配が上がりそうです。
特に今回用いたElastic Netでは、RIDGE回帰とLASSO回帰の影響力の比を調整するハイパーパラメータ\(r\)は\(r=0.5\)で固定しました。
ハイパーパラメータの探索範囲は広がりますが、この\(r\)もチューニングすることで、よりベストな結果を得られるかもしれません。
また明らかに\(r=1\)としたElastic NetはLASSO回帰と等価な問題となります。
その意味でもやはり、実用上はElastic Netをベースとしてモデル選択を行うと良いのではと思います。

小括

本稿ではスパースモデリングの基礎的な概念について紹介しました。
多様な意見はあると前置きしつつ自論を述べると、自然科学の基本的な方針は、一見複雑に見える現象を如何に少数の本質的な組み合わせで解釈できるか、ということにあると私は思います。
組み合わせは往々にして爆発するので一般には困難な場合が多いですが、本稿で紹介したようなスパースモデリングは（データに基づいて）多くの要因の中の少数の要因の組み合わせを発見できうる、大変重要な機械学習の技術であると言えるでしょう。
本稿はスパースモデリング（応用編）へ続きます。
応用編では正則化項\(\Omega(\omega)\)をさらに複雑にし、個々の問題設定に応じたより柔軟なスパースモデリングの手法を紹介します。

参考文献

• 機械学習の炊いたん。 CHAPTER 6 スパース推定の数理　〜オッカムはウィリアムだろ常考〜

• パターン認識と機械学習 上

• スパース性に基づく機械学習

• 岩波データサイエンス Vol．5 スパースモデリングと多変量データ解析

• 機械学習のための連続最適化

• scikit-learn, Uverfitting vs. Overfitting